题目内容
已知函数
．
（1）求满足
的
值；
（2）写出函数
的单调递增区间；
（3）解不等式
（结果用区间表示）．
（1）
（2）
的单调递增区间是
和
（3）
解析:
（1）
，……（1分）
所以，当
时，由得
，
，解得
，
因为，所以
．…………（2分）
当
时，由得
，
，无实数解．……（3分）
所以，满足的值为
．…………（4分）
（2）由
，
当时，的单调递增区间为
；……（6分）
当时，的单调递增区间为
．……（8分）
所以，的单调递增区间是和．…………（9分）
（3）当时，由
得
，…………（12分）
当时，由
得
，恒成立．……（15分）
所以，不等式
的解集为
．……（16分）
练习册系列答案
阅读快车系列答案
相关题目
．
的定义域
；
，求实数
的值．
．
在（0，+∞）上是减函数．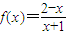
；
成立，若存在求出x；若不存在，请说明理由．
令
的定义域；
的奇偶性，并予以证明；
，猜想
之间的关系并证明.
，
的定义域；（2）证明：
，求
的取值范围。