题目内容
抛物线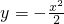 与过点M(0,-1)的直线l相交于A、B两点,O为原点.若OA和OB的斜率之和为1,
与过点M(0,-1)的直线l相交于A、B两点,O为原点.若OA和OB的斜率之和为1,
(1)求直线l的方程; (2)求抛物线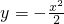 与直线l围成的图形的面积.
与直线l围成的图形的面积.
解:(1)由题意可得直线l的斜率存在,设直线l的方程为y=kx-1,A(x1,y1),B(x2,y2),
所以联立直线与抛物线的方程可得:x2+2kx-2=0,
所以x1+x2=-2k,x1x2=-2,
因为OA和OB的斜率之和为1,即 ,
,
所以 +
+ =
= ,
,
所以k=1,
所以直线方程为y=x-1.
(2)由(1)可得 ,
,
所以 ,
,
因为 ×|x1-x2|,
×|x1-x2|,
所以 .
.
分析:(1)由题意可得设直线l的方程为y=kx-1,联立直线与抛物线的方程可得:x2+2kx-2=0,根据韦达定理可得答案.
(2)由(1)可得 ,结合
,结合 ×|x1-x2|可得答案.
×|x1-x2|可得答案.
点评:本题主要考查直线与抛物线的位置关系,以及三角形的面积公式.
所以联立直线与抛物线的方程可得:x2+2kx-2=0,
所以x1+x2=-2k,x1x2=-2,
因为OA和OB的斜率之和为1,即
 ,
,所以
 +
+ =
= ,
,所以k=1,
所以直线方程为y=x-1.
(2)由(1)可得
 ,
,所以
 ,
,因为
 ×|x1-x2|,
×|x1-x2|,所以
 .
.分析:(1)由题意可得设直线l的方程为y=kx-1,联立直线与抛物线的方程可得:x2+2kx-2=0,根据韦达定理可得答案.
(2)由(1)可得
 ,结合
,结合 ×|x1-x2|可得答案.
×|x1-x2|可得答案.点评:本题主要考查直线与抛物线的位置关系,以及三角形的面积公式.

练习册系列答案
相关题目
 交于A,B两点,若直线OA和直线OB的斜率之和为1。
交于A,B两点,若直线OA和直线OB的斜率之和为1。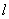 的方程;
的方程;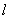 与抛物线相交弦AB的弦长。
与抛物线相交弦AB的弦长。 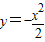 与过点M(0,-1)的直线l相交于A、B两点,O为原点.若OA和OB的斜率之和为1,
与过点M(0,-1)的直线l相交于A、B两点,O为原点.若OA和OB的斜率之和为1,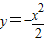 与直线l围成的图形的面积.
与直线l围成的图形的面积.