题目内容
已知函数 在
在 与
与 时都取得极值.
时都取得极值.
(I)求a,b的值及函数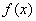 的单调区间;
的单调区间;
(II)若对 ,不等式
,不等式 恒成立,求c的取值范围.
恒成立,求c的取值范围.
解:(I)f(x)=x3+ax2+bx+c,f¢(x)=3x2+2ax+b-------------------------1分
由f¢( )=
)= ,f¢(1)=3+2a+b=0得a=
,f¢(1)=3+2a+b=0得a= ,b=-2
,b=-2
---------------------4分
f¢(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
| x | (-¥, |
| ( | 1 | (1,+¥) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 | ¯ | 极小值 | |

练习册系列答案
相关题目
 中,角
中,角 所对的边分别为
所对的边分别为 ,若
,若

 ,一个焦点的坐标是(0,3),则椭圆的标准方程为( )
,一个焦点的坐标是(0,3),则椭圆的标准方程为( ) B.
B. C.
C.  D.
D.

 ,则函数
,则函数 的导函数为 ( )
的导函数为 ( ) B.
B. C.
C. D.
D.
 满足
满足 ,且
,且 ,则
,则 的解集为
的解集为 B.
B.  C.
C.  D.
D. 
 的前n项和为Sn,若a2 + a4 + a6 = 12,则S7的值是
的前n项和为Sn,若a2 + a4 + a6 = 12,则S7的值是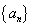 的前
的前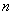 项和为
项和为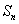 ,满足
,满足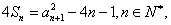 且
且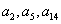 构成等比数列.
构成等比数列.