题目内容
对于函数f(x)定义域中任意的x1、x2（x1≠x2），有如下结论：
①f(x1+x2)=f(x1)·f(x2)；②f(x1·x2)=f(x1)+f(x2);③
＞0;
④f(
)＜
.
当f(x)=10x时，上述结论中正确的序号是_______________.
思路点拨：根据幂的运算法则和指数函数的相关性质分别计算各个式子两端的值,然后比较式子中的等号和不等号是否成立.
解：∵f(x)=10x，且x1≠x2，
∴f(x1+x2)==·
=f(x1)·f(x2).因此,①正确；
f(x1·x2)= 
·x2≠
+
=f(x1)+f(x2).因此,②不正确；
∵函数f(x)=10x是增函数,
∴f(x1)-f(x2)与x1-x2同号.
∴
＞0.因此③正确；
如图.
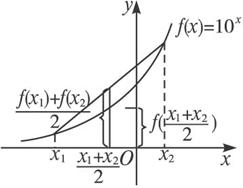
因此④是正确的.综上,填①③④.
练习册系列答案
相关题目
设函数f(x)=2
，对于给定的正数K，定义函数fK(x)=
若对于函数f(x)=2
定义域内的任意 x，恒有fK（x）=f（x），则（ ）
| -x2+x+2 |
|
| -x2+x+2 |
A、K的最大值为2
| ||
B、K的最小值为2
| ||
| C、K的最大值为1 | ||
| D、K的最小值为1 |