题目内容
甲.乙俩人约定上街购物,他们约定在下午4:00到5:00之间在某一街角相会,他们约好当其中一个先到后一定要等另一个人15分钟。若另一个人仍不到则离去,试问这俩人能够相遇的概率为多大?假定他们到达约定地点的时间是随机的且都在约定的一小时之内。
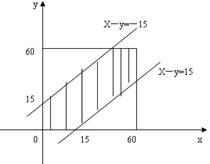
解:设x和y为下午4;00以后甲.乙俩人分别到达约定地点的时间(以分钟计数),则他们所有可能的到达时间都可由有序数对(x,y)来表示,这里0<x<60,0<y<60,基本事件组所对应的几何区域即边长为60的正方形区域(如图),为使得甲.乙俩人相遇他们到达的时间必须在相距15分钟的间隔之内,用数学符号表示即为绝对值不等式x-y<15,而基本事件组所对应的几何区域中x-y<15的图形构成事件r发生的区域,事件r的阴影部分和R的区域如图所示。
因此,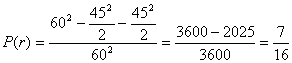

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目