题目内容
x轴上点到A（2，1），B（-2，2）两点距离的最小值为（ ）
| A、3 | ||
B、
| ||
| C、5 | ||
| D、17 |
分析：根据图形的对称可知A′B=A′C+BC=AC+BC最小，利用对称求出A′的坐标，然后利用两点间的距离公式即可求出．
解答：
解：作出A关于x轴的对称点A′，
然后连接A′B与x轴交于C，连接AC，则A′B最小，
所以根据A与A′关于x轴对称得到：A′（2，-1）；
根据两点间的距离公式得A′B=
=5．
故选C．
解：作出A关于x轴的对称点A′，然后连接A′B与x轴交于C，连接AC，则A′B最小，
所以根据A与A′关于x轴对称得到：A′（2，-1）；
根据两点间的距离公式得A′B=
| (-2-2)2+[2-(-1)]2 |
故选C．
点评：考查学生会根据对称找出最短线段的能力，灵活运用两点间的距离公式求值，会找一个点关于x轴的对称点的坐标．同时考查了学生会利用数形结合的数学思想解决实际问题．
练习册系列答案
相关题目
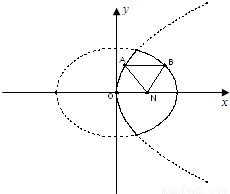
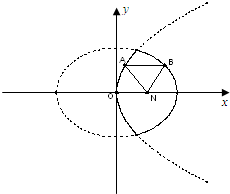[理]如图，已知动点A，B分别在图中抛物线y2=4x及椭圆
已知椭圆C：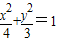
的实线上运动，若AB∥x轴，点N的坐标为（1，0），则△ABN的周长l的取值范围是 ．