题目内容
动圆M过定点A(-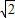 ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-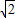 )2+y2=12相切.
)2+y2=12相切.(1)求动圆圆心M的轨迹C的方程;
(2)过点P(0,2)的直线l与轨迹C交于不同的两点E、F,求
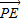 •
•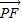 的取值范围.
的取值范围.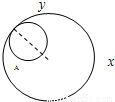
【答案】分析:(1)依题意动圆与定圆相内切,可得|MA´|+|MA|=2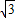 >2
>2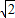 ,利用椭圆定义,即可求出动圆圆心M的轨迹的方程;
,利用椭圆定义,即可求出动圆圆心M的轨迹的方程;
(2)设出直线方程,代入椭圆方程,利用韦达定理即向量数量积公式,即可求得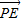 •
•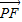 的取值范围.
的取值范围.
解答: 解:(1)A´(
解:(1)A´(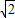 ,0),依题意动圆与定圆相内切,
,0),依题意动圆与定圆相内切,
∴|MA´|+|MA|=2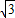 >2
>2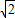 …(3分)
…(3分)
∴点M的轨迹是以A´、A为焦点,2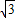 为长轴上的椭圆,
为长轴上的椭圆,
∵a=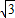 ,c=
,c=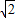
∴b2=1.
∴点M的轨迹方程为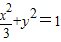 …(5分)
…(5分)
(2)解:设l的方程为x=k(y-2)代入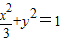 ,消去x得:(k2+3)y2-4k2y+4k2-3=0
,消去x得:(k2+3)y2-4k2y+4k2-3=0
由△>0得16k4-(4k2-3)(k2+3)>0,∴0≤k2<1 …(7分)
设E(x1,y1),F(x2,y2),
则y1+y2=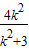 ,y1y2=
,y1y2=
又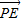 =(x1,y1-2),
=(x1,y1-2),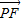 =(x2,y2-2)
=(x2,y2-2)
∴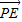 •
• =x1x2+(y1-2)(y2-2)=k(y1-2)•k (y2-2)+(y1-2)(y2-2)
=x1x2+(y1-2)(y2-2)=k(y1-2)•k (y2-2)+(y1-2)(y2-2)
=(1+k2)(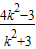 -2×
-2×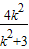 +4)=9(1-
+4)=9(1-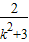 ) …(10分)
) …(10分)
∵0≤k2<1,∴3≤k2+3<4
∴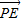 •
•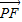 ∈[3,
∈[3, ) …(12分)
) …(12分)
点评:本题考查椭圆的定义,考查轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
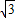 >2
>2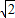 ,利用椭圆定义,即可求出动圆圆心M的轨迹的方程;
,利用椭圆定义,即可求出动圆圆心M的轨迹的方程;(2)设出直线方程,代入椭圆方程,利用韦达定理即向量数量积公式,即可求得
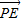 •
•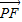 的取值范围.
的取值范围.解答:
 解:(1)A´(
解:(1)A´(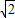 ,0),依题意动圆与定圆相内切,
,0),依题意动圆与定圆相内切,∴|MA´|+|MA|=2
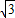 >2
>2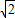 …(3分)
…(3分)∴点M的轨迹是以A´、A为焦点,2
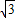 为长轴上的椭圆,
为长轴上的椭圆,∵a=
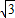 ,c=
,c=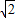
∴b2=1.
∴点M的轨迹方程为
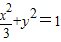 …(5分)
…(5分)(2)解:设l的方程为x=k(y-2)代入
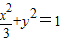 ,消去x得:(k2+3)y2-4k2y+4k2-3=0
,消去x得:(k2+3)y2-4k2y+4k2-3=0由△>0得16k4-(4k2-3)(k2+3)>0,∴0≤k2<1 …(7分)
设E(x1,y1),F(x2,y2),
则y1+y2=
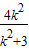 ,y1y2=
,y1y2=
又
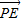 =(x1,y1-2),
=(x1,y1-2),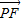 =(x2,y2-2)
=(x2,y2-2)∴
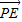 •
• =x1x2+(y1-2)(y2-2)=k(y1-2)•k (y2-2)+(y1-2)(y2-2)
=x1x2+(y1-2)(y2-2)=k(y1-2)•k (y2-2)+(y1-2)(y2-2)=(1+k2)(
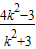 -2×
-2×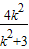 +4)=9(1-
+4)=9(1-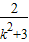 ) …(10分)
) …(10分)∵0≤k2<1,∴3≤k2+3<4
∴
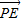 •
•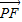 ∈[3,
∈[3, ) …(12分)
) …(12分)点评:本题考查椭圆的定义,考查轨迹方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
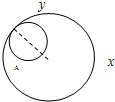 动圆M过定点A(-
动圆M过定点A(- ,0),且与定圆A´:(x-
,0),且与定圆A´:(x- 的取值范围.
的取值范围. ,0),且与定圆A´:(x-
,0),且与定圆A´:(x-
 的取值范围.
的取值范围.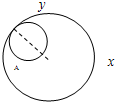 动圆M过定点A(-
动圆M过定点A(- ,0),且与定圆A?:(x-
,0),且与定圆A?:(x-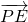 •
• 的取值范围.
的取值范围.