Question

【题目】已知A、B、C是椭圆M： =1（a＞b＞0）上的三点，其中点A的坐标为 ，BC过椭圆M的中心，且 ．
（1）求椭圆M的方程；
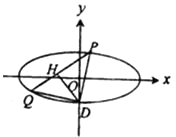
（2）过点（0，t）的直线l（斜率存在时）与椭圆M交于两点P、Q，设D为椭圆M与y轴负半轴的交点，且 ，求实数t的取值范围．

Answer 1

【答案】
（1）解：

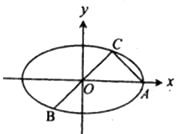
∵点A的坐标为 ，

∴ ，椭圆方程为 ①

又∵ ．，且BC过椭圆M的中心O（0，0），

∴ ．

又∵ ，

∴△AOC是以∠C为直角的等腰三角形，

易得C点坐标为（ ， ）

将（ ， ）代入①式得b2=4

∴椭圆M的方程为

（2）解：当直线l的斜率k=0，直线l的方程为y=t

则满足题意的t的取值范围为﹣2＜t＜2

当直线l的斜率k≠0时，设直线l的方程为y=kx+t

由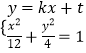

得（3k2+1）x2+6ktx+3t2﹣12=0

∵直线l与椭圆M交于两点P、Q，

∴△=（6kt）2﹣4（3k2+1）（3t2﹣12）＞0

即t2＜4+12k2 ②

设P（x1，y1），Q（x2，y2），x1+x2=﹣ ，x1x2= ，

PQ中点H（x0，y0），

则H的横坐标 ，

纵坐标 ，

D点的坐标为（0，﹣2）

由 ，

得DH⊥PQ，kDHkPQ=﹣1，

即 ，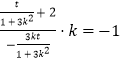

即t=1+3k2． ③

∴k2＞0，∴t＞1． ④

由②③得0＜t＜4，

结合④得到1＜t＜4．

综上所述，﹣2＜t＜4．

【解析】（1）根据点A的坐标求出a，然后根据 求出b，综合即可求出椭圆M的方程．（2）根据题意设出直线方程，与（1）中M的方程联立，然后运用设而不求韦达定理进行计算，求出实数t的取值范围．
【考点精析】认真审题，首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴：，焦点在y轴：)．