题目内容
已知曲线C:y2=x＋1,定点A(3,1),B为C上任一点,点P在线段AB上且有BP∶PA=1∶2,当B在C上运动时,求P点的轨迹方程.
解:设P(x0,y0)是轨迹上任一点,B(x1,y1)是y2=x＋1上任一点,则有
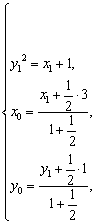即
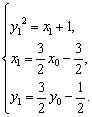
∴所求P点的轨迹方程为(
y0－
)2=(
x0－
)＋1,即(y－
)2=
(x－
).
练习册系列答案
相关题目
已知曲线C：
-
=1，下列叙述中错误的是（ ）
| x|x| |
| a2 |
| y|y| |
| b2 |
| A、垂直于x轴的直线与曲线C只有一个交点 | ||
| B、直线y=kx+m（k，m∈R）与曲线C最多有三个交点 | ||
| C、曲线C关于直线y=-x对称 | ||
D、若P1（x1，y1），P2（x2，y2）为曲线C上任意两点，则有
|
)∪(
，+∞)
，+∞) D．(-∞，-3
)∪(3
，+∞)