题目内容
棱长为1的正方体ABCD—A1B1C1D1中,P为DD1的中点,O1、O2、O3分别为平面A1B1C1D1、平面BB1C1C、平面ABCD的中心.
(1)求PO2的长。
(2)求证:B1O3⊥PA;
(3)求异面直线PO3与O1O2所成的角;

解:以D为坐标原点,以DA,DC,DD1所在直线分别为x轴、y轴、z轴
建立如图所示的空间直角坐标系D—xyz,则 …………2分
B1(1,1,1,),![]()
 于是
于是![]() …………4分
…………4分
(1)由模的公式得:![]()
即PO2的长为![]() …………6分
…………6分
(2)证明:![]()
![]() …………8分
…………8分
(3)![]() ,
,
![]() …………9分
…………9分

 …………11分
…………11分
∴异面直线PO3与O1O3所成角的大小![]() …………12分
…………12分
(此题用几何法同样可以求解,略)

练习册系列答案
相关题目
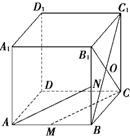 如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,M为AB的中点,N为BB1的中点,O为平面BCC1B1的中心. 已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )
已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为( )