题目内容
下列命题中真命题是( )
A、?x∈R,使得sinxcosx=
| ||
| B、?x∈(-∞,0),2x>1 | ||
| C、?x∈R,x2≥x-1 | ||
| D、?x∈(0,π),sinx>cosx |
分析:根据倍角公式及三角函数的值域,我们可以判断A的正误,根据指数函数的性质,我们可以判断B的真假,解一元二次不等式,可以判断C的正误,根据三角函数的性质,我们可判断D的对错,进而得到答案.
解答:解:∵sinxcosx=
sin2x,若sinxcosx=
,则sin2x=
>1,故A错误;
∵当x∈(-∞,0),2x<1恒成立,故B错误;
∵方程x2-x+1=0的△=1-4=-3<0,函数y=x2-x+1的图象为开口朝上的抛物线,故x2-x+1≥0恒成立,即?x∈R,x2≥x-1,故C正确;
∵当x=
∈∈(0,π),sinx=cosx,故?x∈(0,π),sinx>cosx,故D错误;
故选C
| 1 |
| 2 |
| 3 |
| 5 |
| 6 |
| 5 |
∵当x∈(-∞,0),2x<1恒成立,故B错误;
∵方程x2-x+1=0的△=1-4=-3<0,函数y=x2-x+1的图象为开口朝上的抛物线,故x2-x+1≥0恒成立,即?x∈R,x2≥x-1,故C正确;
∵当x=
| π |
| 4 |
故选C
点评:本题考查的知识点是命题的真假判断与应用,其中利用函数的性质,逐一分析四个结论的正误是解答本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
.已知各项均不为零的数列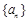 ,定义向量
,定义向量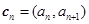 ,
,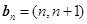 ,
,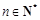 . 下列命题中真命题是
. 下列命题中真命题是
A.若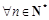 总有 总有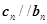 成立,则数列 成立,则数列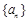 是等差数列 是等差数列 |
B.若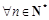 总有 总有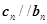 成立,则数列 成立,则数列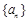 是等比数列 是等比数列 |
C.若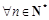 总有 总有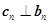 成立,则数列 成立,则数列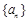 是等差数列 是等差数列 |
D.若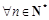 总有 总有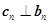 成立,则数列 成立,则数列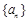 是等比数列 是等比数列 |
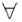 n∈N*总有cn∥bn成立,则数列{an}是等差数列
n∈N*总有cn∥bn成立,则数列{an}是等差数列 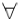 n∈N*总有cn∥bn成立,则数列{an}是等比数列
n∈N*总有cn∥bn成立,则数列{an}是等比数列 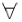 n∈N*总有cn⊥bn成立,则数列{an}是等差数列
n∈N*总有cn⊥bn成立,则数列{an}是等差数列 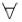 n∈N*总有cn⊥bn成立,则数列{an}是等比数列
n∈N*总有cn⊥bn成立,则数列{an}是等比数列