题目内容
若向量 、
、 满足
满足 =(2,-1),
=(2,-1), =(1,2),则向量
=(1,2),则向量 与
与 的夹角等于________°.
的夹角等于________°.
135
分析:先求出 得坐标,进而求得
得坐标,进而求得 的值,再由两个向量夹角公式cosθ=
的值,再由两个向量夹角公式cosθ= 求出cosθ的值 即可求得向量
求出cosθ的值 即可求得向量 与
与 的夹角θ的值.
的夹角θ的值.
解答:∵ =(2,-1),
=(2,-1), =(1,2),∴
=(1,2),∴ =(2,-1)-(1,2)=(1,-3).
=(2,-1)-(1,2)=(1,-3).
∴ =(1,2)•(1,-3)=1-6=-5.
=(1,2)•(1,-3)=1-6=-5.
设向量 与
与 的夹角等于θ,则有cosθ=
的夹角等于θ,则有cosθ= =
= =-
=- .
.
再由 0°≤θ<180°可得 θ=135°,
故答案为 135°.
点评:本题主要考查两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.
分析:先求出
 得坐标,进而求得
得坐标,进而求得 的值,再由两个向量夹角公式cosθ=
的值,再由两个向量夹角公式cosθ= 求出cosθ的值 即可求得向量
求出cosθ的值 即可求得向量 与
与 的夹角θ的值.
的夹角θ的值.解答:∵
 =(2,-1),
=(2,-1), =(1,2),∴
=(1,2),∴ =(2,-1)-(1,2)=(1,-3).
=(2,-1)-(1,2)=(1,-3).∴
 =(1,2)•(1,-3)=1-6=-5.
=(1,2)•(1,-3)=1-6=-5.设向量
 与
与 的夹角等于θ,则有cosθ=
的夹角等于θ,则有cosθ= =
= =-
=- .
.再由 0°≤θ<180°可得 θ=135°,
故答案为 135°.
点评:本题主要考查两个向量坐标形式的运算,两个向量夹角公式的应用,属于中档题.

练习册系列答案
相关题目
已知向量
=(1,2),
=(2,-3).若向量
满足(
+
)∥
,
⊥(
+
),则
=( )
| a |
| b |
| c |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
 与
与 满足|
满足| |=3,|
|=3,| |=2,
|=2, •
• =3,则
=3,则 与
与 的夹角为 .
的夹角为 .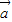 ,
,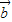 满足|
满足|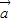 |=1,|
|=1,|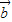 |=2,且
|=2,且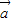 ,
,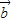 的夹角为
的夹角为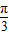 ,则
,则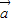 •
• = ,|
= ,| +
+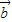 |= .
|= .