题目内容
已知向量
=（1，2），
=（1，0），
=（3，4），若（
+x
）⊥
，则实数x=（ ）
| a |
| b |
| c |
| b |
| a |
| c |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由向量的坐标运算可得
+x
的坐标，由（
+x
）⊥
可得（
+x
）•
=0，解关于x的方程可得．
| b |
| a |
| b |
| a |
| c |
| b |
| a |
| c |
解答：
解：∵向量
=（1，2），
=（1，0），
=（3，4），
∴
+x
=（1，0）+x（1，2）=（1+x，2x），
∵（
+x
）⊥
，∴（
+x
）•
=3（1+x）+8x=0，
解得x=-
故选：A
| a |
| b |
| c |
∴
| b |
| a |
∵（
| b |
| a |
| c |
| b |
| a |
| c |
解得x=-
| 3 |
| 11 |
故选：A
点评：本题考查数量积与向量的垂直关系，属基础题．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形，且∠C1CB=∠C1CD=∠BCD，试问：当
执行如图所示的程序框图，若输入数据n=3，a1=1，a2=2，a3=3，则输出的结果为（ ）| A、4 | B、3 | C、2 | D、1 |
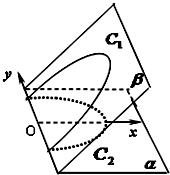如右图二面角α-y-β的大小为60°，平面β上的曲线C1在平面α上的正射影为曲线C2，C2在直角坐标系xOy下的方程x2+y2=1（0≤x≤1），则曲线C1的离心率（ ）| A、e=1 | ||||
| B、e＞1 | ||||
C、e=
| ||||
D、e=
|