题目内容
若两个非零向量 ,
, 满足|
满足| +
+ |=|
|=| -
- |=2|
|=2| |,则向量
|,则向量 +
+ 与
与 -
- 的夹角是
的夹角是
- A.

- B.

- C.

- D.

C
分析:利用向量模的平方等于向量的平方得到两个向量的关系,利用向量的数量积公式求出两向量的夹角.
解答:依题意,∵| +
+ |=|
|=| -
- |=2|
|=2| |
|
∴ =
=
∴ ⊥
⊥ ,
, =3
=3 ,
,
∴cos< ,
, >=
>= =-
=- ,
,
所以向量 与
与 的夹角是
的夹角是 ,
,
故选C
点评:本题考查向量模的平方等于向量的平方、利用向量的数量积公式求向量的夹角.
分析:利用向量模的平方等于向量的平方得到两个向量的关系,利用向量的数量积公式求出两向量的夹角.
解答:依题意,∵|
 +
+ |=|
|=| -
- |=2|
|=2| |
|∴
 =
=
∴
 ⊥
⊥ ,
, =3
=3 ,
,∴cos<
 ,
, >=
>= =-
=- ,
,所以向量
 与
与 的夹角是
的夹角是 ,
,故选C
点评:本题考查向量模的平方等于向量的平方、利用向量的数量积公式求向量的夹角.

练习册系列答案
相关题目
 ,
, 满足
满足 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( ) B.
B. C.
C. D.
D.
 ,
, 满足|
满足| ,则
,则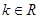 ,且
,且 ,则
,则
 ,则
,则 或
或
 ,满足|
,满足| |
| |
| |,则
|,则
 |
|