题目内容
如图,已知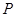 是平行四边形
是平行四边形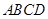 所在平面外一点,
所在平面外一点,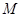 、
、 分别是
分别是 、
、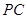 的中点; 求证:
的中点; 求证: 平面
平面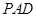

【答案】
证明:取PD的中点E,连接AE,NE。又 M,N分别为中点,
M,N分别为中点, EN∥AM,且EN=AM,
EN∥AM,且EN=AM,
 四边形AMNE是平行四边形,
四边形AMNE是平行四边形, MN∥AE,又AE
MN∥AE,又AE 平面PAD,MN
平面PAD,MN 平面PAD,
平面PAD, MN∥平面PAD。
MN∥平面PAD。
【解析】本题主要考查了线面平行的判定定理,同时考查了空间想象能力,属于基础题.
取PD中点Q,连AQ、QN,根据四边形AMNQ为平行四边形可得MN∥AQ,根据直线与平面平行的判定定理可证得EF∥面PAD

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
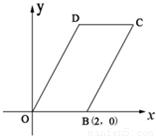
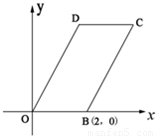
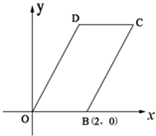 如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.
如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.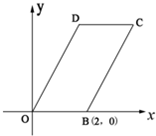 如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.
如图,已知四边形OBCD是平行四边形,|OB|=2,|OD|=4,∠DOB=60°,直线x=t(0<t<4)分别交平行四边行两边于不同的两点M、N.