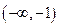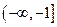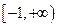题目内容
已知函数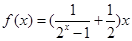 .
.
(1)求函数的定义域;(2)判断函数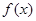 的奇偶性;(3)求证:
的奇偶性;(3)求证: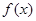 ﹥0.
﹥0.
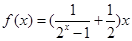 .
.(1)求函数的定义域;(2)判断函数
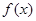 的奇偶性;(3)求证:
的奇偶性;(3)求证: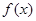 ﹥0.
﹥0.(1) ;(2)偶函数,证明见解析;(3)证明见解析.
;(2)偶函数,证明见解析;(3)证明见解析.
 ;(2)偶函数,证明见解析;(3)证明见解析.
;(2)偶函数,证明见解析;(3)证明见解析.试题分析:(1)由分母
 不能为零得求解即可;(2)在(1)的基础上,只要再判断
不能为零得求解即可;(2)在(1)的基础上,只要再判断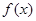 与
与 的关系即可;(3)在(2)的基础上要证明对称区间上成立可即可.不妨证明:当
的关系即可;(3)在(2)的基础上要证明对称区间上成立可即可.不妨证明:当 时,则有
时,则有 进而有
进而有 ,
, ,然后得到
,然后得到 ,再由奇偶性得到对称区间上的结论.
,再由奇偶性得到对称区间上的结论.试题解析:(1)
 .
.(2)设

 ,
, ,
, 为偶函数.
为偶函数.(3)当
 时,
时, <
< <1,
<1, -1<
-1< <0,
<0, <
< .
.又
 ,则
,则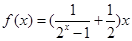 >0,
>0,由
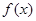 为偶函数知,当x>0时,
为偶函数知,当x>0时,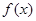 >0,
>0,综上可知当
 >0.
>0.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
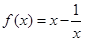 .
.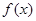 的奇偶性,并加以证明;
的奇偶性,并加以证明;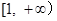 上为增函数;
上为增函数;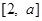 上的最大值与最小值之和不小于
上的最大值与最小值之和不小于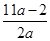 ,求
,求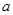 的取值范围.
的取值范围.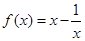 ,
, .
.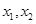 ,其中
,其中 ,求
,求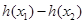 的最小值.
的最小值. ,下列结论不正确的( )
,下列结论不正确的( ) .若
.若 ,则( )
,则( )



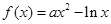 存在垂直于
存在垂直于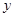 轴的切线,则实数
轴的切线,则实数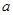 的取值范围是_______.
的取值范围是_______. 在区间
在区间 上具有单调性,则实数
上具有单调性,则实数 的取值范围是 .
的取值范围是 . (a为常数).若
(a为常数).若 在区间[-1,+∞)上是增函数,则a的取值范围是( )
在区间[-1,+∞)上是增函数,则a的取值范围是( )