题目内容
给出下列命题,其中正确的命题是 (写出所有正确命题的编号).
①在 中,若
中,若 ,则
,则 是锐角三角形;
是锐角三角形;
②在 中,
中, 是
是 的充要条件;
的充要条件;
③已知非零向量 ,则“
,则“ ”是“
”是“ 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;
④命题“在三棱锥 中,已知
中,已知 ,若点
,若点 在
在 所在的平面内,则
所在的平面内,则 ”的否命题为真命题;
”的否命题为真命题;
⑤函数 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数,那么
为恒均变函数,那么 为恒均变函数
为恒均变函数
①在
 中,若
中,若 ,则
,则 是锐角三角形;
是锐角三角形;②在
 中,
中, 是
是 的充要条件;
的充要条件;③已知非零向量
 ,则“
,则“ ”是“
”是“ 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;④命题“在三棱锥
 中,已知
中,已知 ,若点
,若点 在
在 所在的平面内,则
所在的平面内,则 ”的否命题为真命题;
”的否命题为真命题;⑤函数
 的导函数为
的导函数为 ,若对于定义域内任意
,若对于定义域内任意 ,
,
 ,有
,有 恒成立,则称
恒成立,则称 为恒均变函数,那么
为恒均变函数,那么 为恒均变函数
为恒均变函数①②④⑤
因为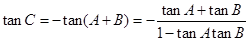
所以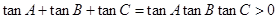 ,则
,则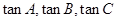 中有两个为负或全为正。因为
中有两个为负或全为正。因为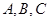 是三角形内角,至多只有一个钝角即
是三角形内角,至多只有一个钝角即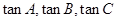 中至多只有一个为负,所以
中至多只有一个为负,所以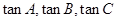 全为正,即
全为正,即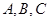 都是锐角,所以
都是锐角,所以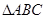 是锐角三角形,命题①正确;
是锐角三角形,命题①正确;
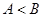 ,显然
,显然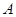 一定是锐角。若
一定是锐角。若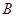 为钝角或直角,则
为钝角或直角,则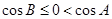 。若
。若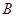 为锐角,因为函数
为锐角,因为函数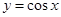 在区间
在区间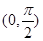 单调递减,所以
单调递减,所以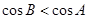 。所以
。所以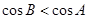 。反之,
。反之,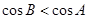 ,若
,若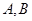 都是锐角,由函数
都是锐角,由函数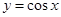 在区间
在区间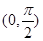 单调递减可得
单调递减可得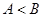 。若
。若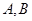 之中有一个为钝角或直角,则这个角是
之中有一个为钝角或直角,则这个角是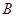 ,故
,故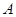 是锐角,所以
是锐角,所以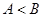 。综上可得,
。综上可得,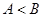 ,故命题②正确;
,故命题②正确;
若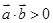 ,则
,则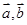 夹角为锐角或
夹角为锐角或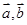 同向,反之若
同向,反之若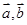 夹角为锐角,根据向量积运算可得
夹角为锐角,根据向量积运算可得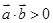 ,所以“
,所以“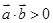 ”是“
”是“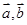 夹角为锐角”必要不充分条件,故命题③不正确;
夹角为锐角”必要不充分条件,故命题③不正确;
命题“在三棱锥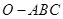 中,已知
中,已知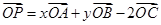 ,若点
,若点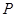 在
在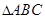 所在的平面内,则
所在的平面内,则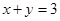 ”的否命题为真命题,故命题④正确;
”的否命题为真命题,故命题④正确;
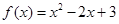 ,则
,则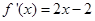 ,故
,故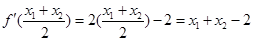
而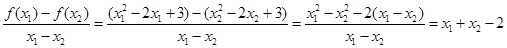
所以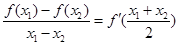 恒成立,故命题⑤正确。
恒成立,故命题⑤正确。
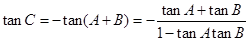
所以
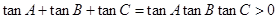 ,则
,则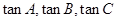 中有两个为负或全为正。因为
中有两个为负或全为正。因为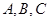 是三角形内角,至多只有一个钝角即
是三角形内角,至多只有一个钝角即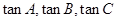 中至多只有一个为负,所以
中至多只有一个为负,所以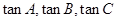 全为正,即
全为正,即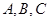 都是锐角,所以
都是锐角,所以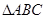 是锐角三角形,命题①正确;
是锐角三角形,命题①正确;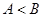 ,显然
,显然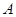 一定是锐角。若
一定是锐角。若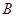 为钝角或直角,则
为钝角或直角,则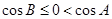 。若
。若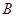 为锐角,因为函数
为锐角,因为函数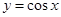 在区间
在区间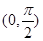 单调递减,所以
单调递减,所以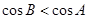 。所以
。所以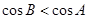 。反之,
。反之,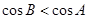 ,若
,若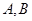 都是锐角,由函数
都是锐角,由函数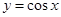 在区间
在区间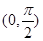 单调递减可得
单调递减可得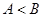 。若
。若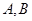 之中有一个为钝角或直角,则这个角是
之中有一个为钝角或直角,则这个角是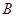 ,故
,故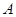 是锐角,所以
是锐角,所以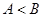 。综上可得,
。综上可得,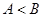 ,故命题②正确;
,故命题②正确;若
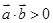 ,则
,则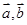 夹角为锐角或
夹角为锐角或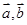 同向,反之若
同向,反之若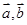 夹角为锐角,根据向量积运算可得
夹角为锐角,根据向量积运算可得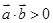 ,所以“
,所以“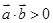 ”是“
”是“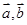 夹角为锐角”必要不充分条件,故命题③不正确;
夹角为锐角”必要不充分条件,故命题③不正确;命题“在三棱锥
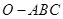 中,已知
中,已知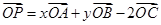 ,若点
,若点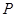 在
在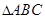 所在的平面内,则
所在的平面内,则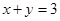 ”的否命题为真命题,故命题④正确;
”的否命题为真命题,故命题④正确;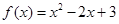 ,则
,则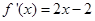 ,故
,故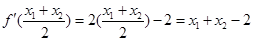
而
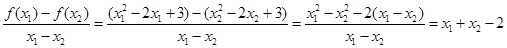
所以
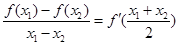 恒成立,故命题⑤正确。
恒成立,故命题⑤正确。
练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
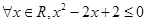 ”的否定为( )
”的否定为( )



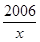 在区间(-
在区间(-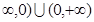 上是单调递减的;
上是单调递减的;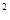 +2x+1在区间(0,+
+2x+1在区间(0,+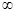 )上是单调递增的;
)上是单调递增的;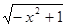 在区间
在区间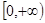 上是单调递减的;
上是单调递减的; ”改写成“若p则q”的形式:
”改写成“若p则q”的形式: 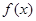 的定义域为R,若
的定义域为R,若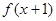 是奇函数,
是奇函数,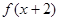 是偶函数. 下列四个结论:
是偶函数. 下列四个结论: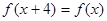 ②
②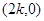 对称
对称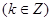
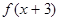 是奇函数 ④
是奇函数 ④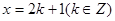 对称
对称 是偶函数,但不是奇函数;
是偶函数,但不是奇函数; 中,若
中,若 ,则
,则
 ;
; ,则
,则 ;
;  定义域为R,且
定义域为R,且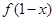 =
= ,则
,则 轴对称;
轴对称;  的图象和直线
的图象和直线 的公共点不可能是1个.
的公共点不可能是1个.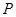 :对任意实数
:对任意实数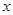 都有
都有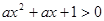 恒成立;
恒成立;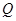 :关于
:关于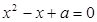 有实数根.如果
有实数根.如果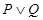 为真命题,
为真命题,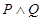 为假命题,求实数
为假命题,求实数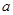 的取值范围。
的取值范围。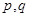 是两个命题,
是两个命题,
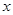 的不等式
的不等式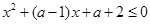 的解集为A .
的解集为A .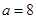 , 求A ;
, 求A ; , 求实数
, 求实数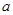 的取值范围;
的取值范围; ”是“
”是“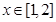 ”的必要不充分条件, 求实数
”的必要不充分条件, 求实数