题目内容
已知函数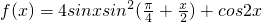 .
.
(I)设ω>0为常数,若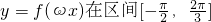 上是增函数,求ω的取值范围
上是增函数,求ω的取值范围
(II)若|f(x)-m|<2成立的充分条件是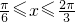 ,求实数m的取值范围.
,求实数m的取值范围.
解:(I)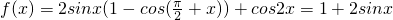 …3分
…3分
由题意,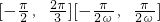 ,
,
只须 ,?ω≤
,?ω≤ ,又ω>0,
,又ω>0,
∴ ,
,
得ω的取值范围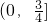 …6分
…6分
(II)由题意,当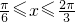 时,
时, ≤sinx≤1,
≤sinx≤1,
2sinx-1<m<2sinx+3恒成立 …8分
可得(2sinx-1)max<m<(2sinx+3)min
当sinx=1时,(2sinx-1)max=1;
当sinx= 时,(2sinx+3)min=4;
时,(2sinx+3)min=4;
∴1<m<4…10分.
∴实数m的取值范围1<m<4.
分析:(1)化简函数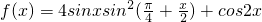 ,然后利用
,然后利用 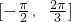 是函数增区间的子集,解答即可.
是函数增区间的子集,解答即可.
(2)先求|f(x)-m|<2中的m的范围表达式,f(x)-2<m<f(x)+2,m大于f(x)-2的最大值,小于f(x)+2的最小值,即可.
点评:本题考查正弦函数的定义域和值域,子集知识,不等式的解法等基础知识,考查运算求解能力,化归与转化思想,是中档题.
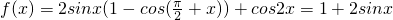 …3分
…3分由题意,
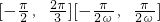 ,
,只须
 ,?ω≤
,?ω≤ ,又ω>0,
,又ω>0,∴
 ,
,得ω的取值范围
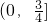 …6分
…6分(II)由题意,当
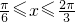 时,
时, ≤sinx≤1,
≤sinx≤1,2sinx-1<m<2sinx+3恒成立 …8分
可得(2sinx-1)max<m<(2sinx+3)min
当sinx=1时,(2sinx-1)max=1;
当sinx=
 时,(2sinx+3)min=4;
时,(2sinx+3)min=4;∴1<m<4…10分.
∴实数m的取值范围1<m<4.
分析:(1)化简函数
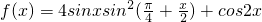 ,然后利用
,然后利用 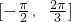 是函数增区间的子集,解答即可.
是函数增区间的子集,解答即可.(2)先求|f(x)-m|<2中的m的范围表达式,f(x)-2<m<f(x)+2,m大于f(x)-2的最大值,小于f(x)+2的最小值,即可.
点评:本题考查正弦函数的定义域和值域,子集知识,不等式的解法等基础知识,考查运算求解能力,化归与转化思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的取值范围;
的取值范围; ,若在
,若在 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数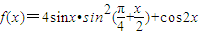 .
. 上是增函数,求ω的取值范围
上是增函数,求ω的取值范围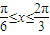 ,求实数m的取值范围.
,求实数m的取值范围.