题目内容
设函数f（x）=-x3+bx（b为常数），若方程f（x）=0的根都在区间[-2，2]内，且函数f（x）在区间（0，1）上单调递增，则b的取值范围是________．
[3，4]
分析：根据函数在一个区间上有三个根，把函数分解因式，得到函数的三个根的表示情况，写出b的范围，再把函数求导，根据在一个区间上递增，写出函数的导函数恒大于零，得到范围．
解答：∵函数f（x）=-x3+bx（b为常数），
∴f（x）=x（-x2+b）=0的三个根都在区间[-2，2]内，
∴
，
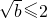b≤4
函数f（x）在区间（0，1）上单调递增，
∴f′（x）=-3x2+b＞0在区间（0，1）上恒成立，
∴b≥3
综上可知3≤b≤4，
故答案为：[3，4]
点评：本题考查利用函数的导函数求函数的单调性，本题解题的关键是写出导函数利用恒成立问题来解决．
分析：根据函数在一个区间上有三个根，把函数分解因式，得到函数的三个根的表示情况，写出b的范围，再把函数求导，根据在一个区间上递增，写出函数的导函数恒大于零，得到范围．
解答：∵函数f（x）=-x3+bx（b为常数），
∴f（x）=x（-x2+b）=0的三个根都在区间[-2，2]内，
∴
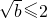，b≤4
函数f（x）在区间（0，1）上单调递增，
∴f′（x）=-3x2+b＞0在区间（0，1）上恒成立，
∴b≥3
综上可知3≤b≤4，
故答案为：[3，4]
点评：本题考查利用函数的导函数求函数的单调性，本题解题的关键是写出导函数利用恒成立问题来解决．
练习册系列答案
相关题目
设函数f（x）的定义域为A，若存在非零实数t，使得对于任意x∈C（C⊆A），有x+t∈A，且f（x+t）≤f（x），则称f（x）为C上的t低调函数．如果定义域为[0，+∞）的函数f（x）=-|x-m2|+m2，且 f（x）为[0，+∞）上的10低调函数，那么实数m的取值范围是（ ）
| A、[-5，5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|