题目内容
在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
,
(Ⅰ)求 的大小;
的大小;
(Ⅱ)若 ,求
,求 的取值范围.
的取值范围.
①. . ②.
. ②.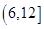 .
.
解析试题分析:①运用正弦定理把边转化成角再求角,②方法一:利用第一问的结论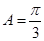 及
及 的条件,只要找到
的条件,只要找到 的取值范围即可,利用余弦定理建立
的取值范围即可,利用余弦定理建立 的关系式,再求
的关系式,再求 的取值范围,方法二,利用正弦定理建立
的取值范围,方法二,利用正弦定理建立 与角
与角 的三角函数关系式,再利用
的三角函数关系式,再利用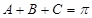 减少变元,求范围.
减少变元,求范围.
试题解析:(Ⅰ)由条件结合正弦定理得,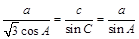
从而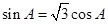 ,
,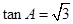
∵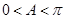 ,∴
,∴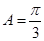 5分
5分
(Ⅱ)法一:由已知: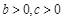 ,
,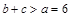
由余弦定理得: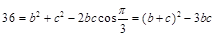
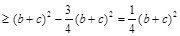
(当且仅当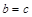 时等号成立)
时等号成立)
∴(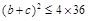 ,又
,又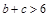 ,
,
∴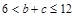 ,
,
从而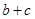 的取值范围是
的取值范围是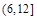 12分
12分
法二:由正弦定理得: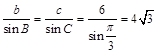
∴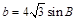 ,
,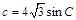 ,
,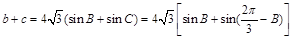
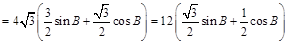
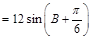
∵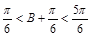
∴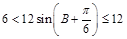 ,即
,即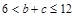 (当且仅当
(当且仅当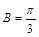 时,等号成立)
时,等号成立)
从而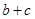 的取值范围是
的取值范围是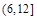 12分
12分
考点:1 正弦定理;2 余弦定理;3 两角和公式;4 均值不等式

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
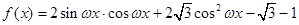 (其中
(其中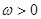 ),
),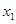 、
、 是函数
是函数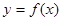 的两个不同的零点,且
的两个不同的零点,且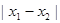 的最小值为
的最小值为 .
. 的值;
的值;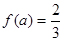 ,求
,求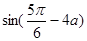 的值.
的值. .
.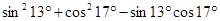 ;
;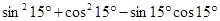 ;
; 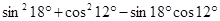 ;
;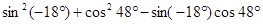 ;
;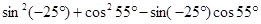 .
.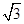 sinωxcosωx(ω>0)的最小正周期为π,
sinωxcosωx(ω>0)的最小正周期为π,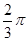 ]上的值域.
]上的值域. 函数
函数 的最小正周期为
的最小正周期为 .
.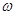 的值;
的值; 在区间
在区间 上的值域.
上的值域.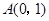 ,
,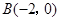 ,
,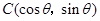 (
(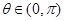 ),
),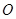 为坐标原点,向量
为坐标原点,向量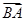 与向量
与向量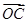 共线.
共线.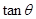 的值;
的值;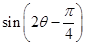 的值.
的值.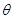 的直线
的直线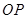 与单位圆在第一象限的部分交于点
与单位圆在第一象限的部分交于点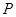 ,单位圆与坐标轴交于点
,单位圆与坐标轴交于点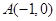 ,点
,点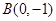 ,
,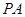 与
与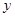 轴交于点
轴交于点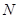 ,
, 与
与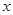 轴交于点
轴交于点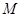 ,设
,设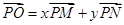
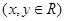
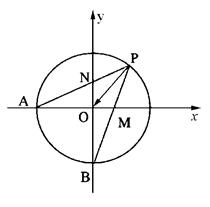
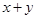 的最小值.
的最小值.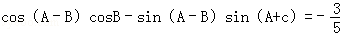 .
.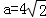 ,b=5,求向量
,b=5,求向量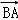 在
在 方向上的投影.
方向上的投影.
 的最小正周期及最大值;
的最小正周期及最大值;
 ,且
,且 ,求
,求 的值.
的值.