题目内容
已知△ABC的内角A、B、C所对的边分别为a、b、c,且a=2,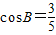 .
.(Ⅰ)若b=4,求sinA的值;
(Ⅱ)若△ABC的面积S=4,求b、c的值.
【答案】分析:本题考查的知识点是正弦定理与余弦定理,
(1)由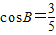 ,我们易求出B的正弦值,再结合a=2,b=4,由正弦定理易求sinA的值;
,我们易求出B的正弦值,再结合a=2,b=4,由正弦定理易求sinA的值;
(2)由△ABC的面积S=4,我们可以求出c值,再由余弦定理可求出b值.
解答:解:(I)∵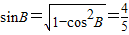 (2分)
(2分)
由正弦定理得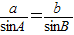 .
.
∴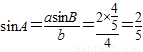 .(5分)
.(5分)
(II)∵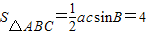 ,
,
∴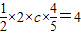 .
.
∴c=5(7分)
由余弦定理得b2=a2+c2-2accosB,
∴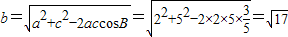 (10分)
(10分)
点评:在解三角形时,正弦定理和余弦定理是最常用的方法,正弦定理多用于边角互化,使用时要注意一般是等式两边是关于三边的齐次式.而余弦定理在使用时一般要求两边有平方和的形式.
(1)由
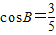 ,我们易求出B的正弦值,再结合a=2,b=4,由正弦定理易求sinA的值;
,我们易求出B的正弦值,再结合a=2,b=4,由正弦定理易求sinA的值;(2)由△ABC的面积S=4,我们可以求出c值,再由余弦定理可求出b值.
解答:解:(I)∵
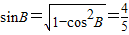 (2分)
(2分)由正弦定理得
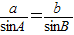 .
.∴
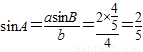 .(5分)
.(5分)(II)∵
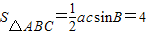 ,
,∴
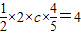 .
.∴c=5(7分)
由余弦定理得b2=a2+c2-2accosB,
∴
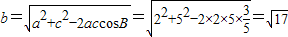 (10分)
(10分)点评:在解三角形时,正弦定理和余弦定理是最常用的方法,正弦定理多用于边角互化,使用时要注意一般是等式两边是关于三边的齐次式.而余弦定理在使用时一般要求两边有平方和的形式.

练习册系列答案
相关题目