题目内容
【题目】动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,设
,设![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)设点![]() ,过点
,过点![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,直线
两点,直线![]() 的斜率分别为
的斜率分别为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() (Ⅱ)1
(Ⅱ)1
【解析】
(1)设Q(x,y),则P(x,2y),代入x2=2y得出轨迹方程;
(2)联立直线AB方程与Q的轨迹方程,得出A,B的坐标关系,代入斜率公式化简|k1﹣k2|,利用二次函数的性质求出最小值.
(Ⅰ)设点![]() ,则由
,则由![]() 得
得![]() ,因为点
,因为点![]() 在抛物线
在抛物线![]() 上,
上,![]()
(Ⅱ)方法一:由已知,直线![]() 的斜率一定存在,设点
的斜率一定存在,设点![]() ,
,
联立![]() 得
得![]()
由韦达定理得![]()
(1)当直线![]() 经过点
经过点![]() 即
即![]() 或
或![]() 时,当
时,当![]() 时,直线
时,直线![]() 的斜率看作抛物线在点
的斜率看作抛物线在点![]() 处的切线斜率,则
处的切线斜率,则![]() ,此时
,此时![]() ;当
;当![]() 时,同理可得
时,同理可得![]()
(2)当直线![]() 不经过点
不经过点![]() 即
即![]() 且
且![]() 时,
时,![]() ,
,
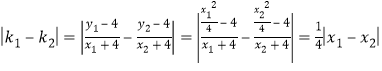
![]()
![]()
![]()
所以![]() 的最小值为
的最小值为![]() .
.
方法二:同上
![]()
![]()
![]()
故![]() ,所以
,所以![]() 的最小值为
的最小值为![]()
方法三:设点![]() ,由直线
,由直线![]() 过点
过点![]() 交轨迹
交轨迹![]() 于
于![]() 两点得:
两点得: 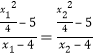 化简整理得:
化简整理得:
![]() ,令
,令![]() ,则
,则![]()
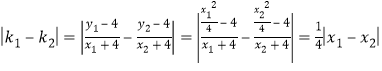
![]()

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目



