Question

【题目】已知椭圆C： =1（a＞b＞0）的右焦点为F，过点F的直线交y轴于点N，交椭圆C于点A、P（P在第一象限），过点P作y轴的垂线交椭圆C于另外一点Q．若 ．

（1）设直线PF、QF的斜率分别为k、k'，求证： 为定值；
（2）若 且△APQ的面积为 ，求椭圆C的方程．

Answer 1

【答案】
（1）解：设焦点F（c，0），由c2=a2﹣b2，P（x1，y1），则Q（﹣x2，y2），

∴直线PF的斜率k= ，QF的斜率k'= ，

∵ ．

∴c=2（x2﹣c），即x2= c

∴k= = ，k'= = ，

∴k=﹣5k'，即 =﹣5为定值．

（2）解：若 ， 则丨AF丨=3丨FP丨，

，解得：A（﹣ c，﹣3y1）

∵点A、P在椭圆C上，则 ，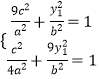

整理得： =8，解得： = ，

则 ，代入得： = ， = ，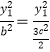

∵△APQ的面积为S△APQ= 3c4y1=6cy1= ，

解得：c2 = ，

∴c2=4，

∴椭圆方程为：

【解析】（1）由题意可知：设P（x1 ， y1），则Q（﹣x2 ， y2），由 ．解得：x2= c，由直线的斜率公式k= = ，k'= = ， =﹣5为定值；（2）由 ， ， ，求得A点坐标，代入椭圆方程，解得 = ，由c2=a2﹣b2 ， ，因此 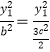= ， = ，由三角形的面积公式可知：S△APQ= 3c4y1=6cy1= ，求得c2 = ，即可求得c的值，求得椭圆方程．