题目内容
12.“$\frac{ln3-5}{3}$≤k≤$\frac{ln2-1}{2}$”是“关于x的不等式lnx+x+1>x2+kx有且仅有2个正整数解”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由图可求得“关于x的不等式lnx+x+1>x2+kx有且仅有2个正整数解”的k的取值范围,结合充要条件的定义,可得答案.
解答 解:关于x的不等式lnx+x+1>x2+kx
即$\frac{lnx}{x}$$+1+\frac{1}{x}$-x>k,
设y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x,
则y′=$\frac{{x}^{2}+lnx}{{x}^{2}}$,
令y′=-$\frac{{x}^{2}+lnx}{{x}^{2}}$的零点为a,则a∈(0,1),且
当x∈(0,a)时,y′>0,y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x为增函数,
当x∈(a,+∞)时,y′>0,y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x为减函数,
故函数y=$\frac{lnx}{x}$$+1+\frac{1}{x}$-x的图象如下图所示: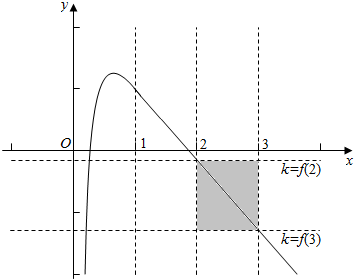
要使$\frac{lnx}{x}$$+1+\frac{1}{x}$-x>k有且仅有2个正整数解,
则k∈[$\frac{ln3}{3}+1+\frac{1}{3}-3$,$\frac{ln2}{2}+1+\frac{1}{2}-2$),
即$\frac{ln3-5}{3}$≤k<$\frac{ln2-1}{2}$”,
故“$\frac{ln3-5}{3}$≤k≤$\frac{ln2-1}{2}$”是“关于x的不等式lnx+x+1>x2+kx有且仅有2个正整数解”的必要不充分条件,
故选:B.
点评 本题考查的知识点是充要条件的定义,存在性问题,数形结合思想,其中求出“关于x的不等式lnx+x+1>x2+kx有且仅有2个正整数解”的充要条件,难度较大.

练习册系列答案
相关题目
17.急剧增加的人口已经使我们赖以生存的地球不堪重负,控制人口急剧增长的急迫任务摆在我们面前.
(1)世界人口在过去的40 年内翻了一番,问每年人口平均增长率是多少?
(2)我国人口在2003年底达到13.14亿,若将人口平均增长率控制在1%以内,我国人口在2013年底最多有多少亿?
以下对数值可供计算使用:
(1)世界人口在过去的40 年内翻了一番,问每年人口平均增长率是多少?
(2)我国人口在2003年底达到13.14亿,若将人口平均增长率控制在1%以内,我国人口在2013年底最多有多少亿?
以下对数值可供计算使用:
| N | 1.010 | 1.015 | 1.017 | 1.310 | 2.000 |
| lgN | 0.0043 | 0.0065 | 0.0075 | 0.1173 | 0.3010 |
| N | 12.48 | 13.11 | 13.14 | 14.51 | |
| lgN | 1.0962 | 1.1176 | 1.1186 | 1.1616 |
 空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.
空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.