题目内容
(本小题满分12分)如图,在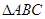 中,
中,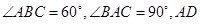 是
是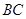 上的高,沿
上的高,沿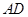 把
把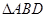 折起,使
折起,使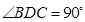 。
。
(Ⅰ)证明:平面ADB ⊥平面BDC;
(Ⅱ)设E为BC的中点,求AE与DB夹角的余弦值。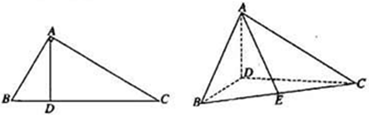
 中,
中,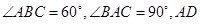 是
是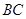 上的高,沿
上的高,沿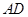 把
把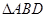 折起,使
折起,使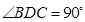 。
。(Ⅰ)证明:平面ADB ⊥平面BDC;
(Ⅱ)设E为BC的中点,求AE与DB夹角的余弦值。

(Ⅰ)见解析;(Ⅱ)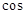 <
<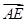 ,
,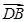 >=
>=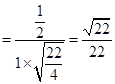 .
.
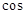 <
<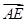 ,
,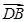 >=
>=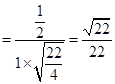 .
. 此题主要考查面面垂直和异面直线夹角公式的求法,第二问解题的关键是作出辅助线,此题是一道中档题,也是高考必考题;(1)已知在△ABC中,AD是BC上的高,沿AD把△ABC折起,使∠BDC=60°,可得AD⊥DC,AD⊥DB,根据面面垂直的判定定理进行求解;
(2)作辅助线,取DC中点F,连接EF,则EF∥BD,可得∠AEF为异面直线AE与BD所成的角,再根据余弦定理和向量公式进行求解;
解(Ⅰ)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,又DB DC=D,
DC=D,
∴AD⊥平面BDC,∵AD 平面 平面BDC.
平面BDC. 平面ABD
平面ABD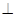 平面BDC。----4分
平面BDC。----4分
(Ⅱ)由∠ BDC= 及(Ⅰ)知DA,DB,DC两两垂直,不防设
及(Ⅰ)知DA,DB,DC两两垂直,不防设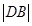 =1,以D为坐标原点,以
=1,以D为坐标原点,以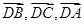 所在直线
所在直线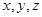 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
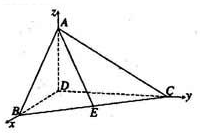
易得D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,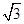 ),E(
),E(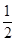 ,
,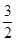 ,0),
,0),
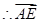 =
=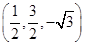 ,
,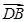 =(1,0,0,),
=(1,0,0,),
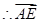 与
与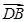 夹角的余弦值为
夹角的余弦值为
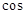 <
<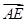 ,
,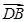 >=
>=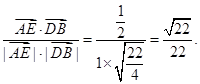
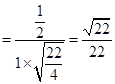 .--------12分
.--------12分
(2)作辅助线,取DC中点F,连接EF,则EF∥BD,可得∠AEF为异面直线AE与BD所成的角,再根据余弦定理和向量公式进行求解;
解(Ⅰ)∵折起前AD是BC边上的高,
∴ 当Δ ABD折起后,AD⊥DC,AD⊥DB,又DB
 DC=D,
DC=D,∴AD⊥平面BDC,∵AD 平面
 平面BDC.
平面BDC. 平面ABD
平面ABD 平面BDC。----4分
平面BDC。----4分(Ⅱ)由∠ BDC=
 及(Ⅰ)知DA,DB,DC两两垂直,不防设
及(Ⅰ)知DA,DB,DC两两垂直,不防设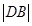 =1,以D为坐标原点,以
=1,以D为坐标原点,以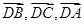 所在直线
所在直线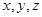 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
易得D(0,0,0),B(1,0,0),C(0,3,0),A(0,0,
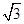 ),E(
),E(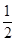 ,
,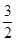 ,0),
,0),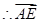 =
=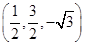 ,
,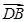 =(1,0,0,),
=(1,0,0,),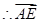 与
与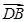 夹角的余弦值为
夹角的余弦值为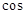 <
<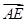 ,
,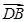 >=
>=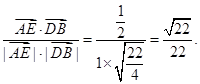
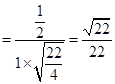 .--------12分
.--------12分
练习册系列答案
相关题目
 所在平面与直角梯形ABCD所在平面互相垂直,
所在平面与直角梯形ABCD所在平面互相垂直, ,
,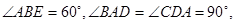 点
点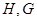 分别是线段
分别是线段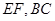 的中点.
的中点. 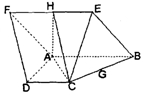
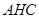
 平面
平面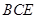 ;
;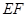 上是否存在点
上是否存在点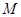 ,使得
,使得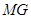
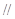 平面
平面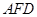 ,若存在,求
,若存在,求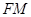 的长并证明;若不存在,说明理由.
的长并证明;若不存在,说明理由.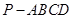 中,底面
中,底面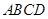 为平行四边形,
为平行四边形,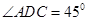 ,
,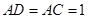 ,
, 为
为 中点,
中点, 平面
平面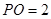 ,
,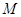 为
为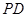 中点.
中点.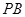 //平面
//平面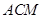 ;
;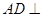 平面
平面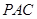 ;
;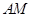 与平面
与平面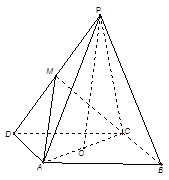
 中,
中, ,
, 是
是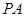 和
和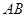 的中点.(Ⅰ)求证:
的中点.(Ⅰ)求证: 平面
平面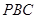 ;
;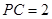 ,求
,求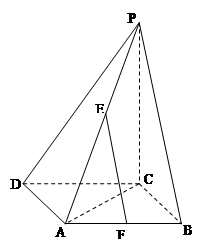
 、
、 分别是正三棱柱
分别是正三棱柱 的棱
的棱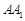 、
、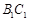 的中点,且棱
的中点,且棱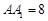 ,
,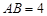 .
.
 平面
平面 ;
; ,使二面角
,使二面角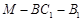 的大小为
的大小为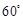 ,若存在,求
,若存在,求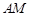 的长;若不存在,说明理由。
的长;若不存在,说明理由。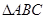 内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①
内接于圆O,且AB为圆O的直径,点M为线段PB的中点.现有以下命题:①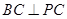 ;②
;②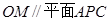 ;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )
;③点A到平面PBC距离就是△PAC的PC边上的高.④二面角P-BC-A大小不可能为450,其中真命题的个数为 ( )
 与平面
与平面 ,有以下四个命题:
,有以下四个命题: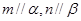 且
且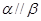 ,则
,则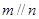 ;
;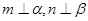 且
且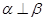 ,则
,则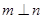 ;
;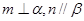 且
且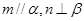 且
且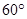 的菱形
的菱形 沿较短对角线
沿较短对角线 折成四面体
折成四面体 分别为
分别为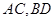 的中点,则下列命题中正确的是 。
的中点,则下列命题中正确的是 。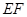 ∥
∥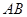 ;②
;②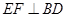 ;③
;③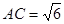 ; ⑤
; ⑤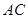 垂直于截面
垂直于截面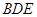 .
. 是不同的直线,
是不同的直线,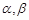 是不同的平面,若①
是不同的平面,若①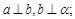 ②
②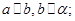 ③
③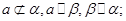 ④
④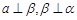 ,则其中能使
,则其中能使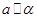 的充分条件的个数为( )
的充分条件的个数为( )