题目内容
(本小题满分12分)
在 中,角
中,角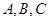 所对的边分别为
所对的边分别为 ,且满足
,且满足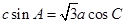 .
.
(1)求角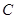 的大小;
的大小;
(2)求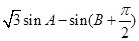 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角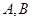 的大小.
的大小.
(1) (2)最大值为1,此时
(2)最大值为1,此时
解析试题分析:(1)由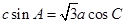 结合正弦定理得,
结合正弦定理得, , ……2分
, ……2分
从而 ,
, , ……4分
, ……4分
∵ ,∴
,∴ ; ……6分
; ……6分
(2)由(1)知 , ……7分
, ……7分
∴ ……8分
……8分
 ……9分
……9分
 , ……10分
, ……10分
∵ ,∴
,∴ ,
,
当 时,
时,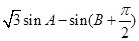 取得最大值, ……11分
取得最大值, ……11分
此时 . ……12分
. ……12分
考点:本小题主要考查正弦定理,余弦定理,三角函数的化简和三角函数的图象和性质.
点评:高考中经常将三角函数和向量结合正弦定理、余弦定理出题考查,难度一般不大,但是三角函数中公式比较多,要牢固掌握,灵活选择应用,还要注意各个公式的适用条件.

练习册系列答案
相关题目
 的三个内角
的三个内角 对应的三条边长分别是
对应的三条边长分别是 ,且满足
,且满足
 的值;
的值; ,
,  ,求
,求 和
和 的值.
的值.
 ,并且
,并且
 的递增区间。
的递增区间。 =" (2a,C" -26) ,
=" (2a,C" -26) ,  = (cosC,l),且
= (cosC,l),且 北偏东
北偏东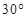 方向的点
方向的点 处有一观测站,港口正东方向的
处有一观测站,港口正东方向的 处有一轮船,测得
处有一轮船,测得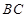 为
为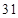 海里.该轮船从
海里.该轮船从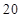 海里后到达
海里后到达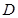 处,测得
处,测得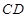 为
为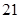 海里. 问此时轮船离港口
海里. 问此时轮船离港口
 中,角A,B,C的对边分别是
中,角A,B,C的对边分别是 且满足
且满足
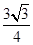 且
且 ,求
,求 的值;
的值; ,已知坐标原点与顶点B重合,且
,已知坐标原点与顶点B重合,且 ,
, ,
, =
= ,且∠A为锐角。(12分)
,且∠A为锐角。(12分)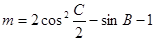 ,求实数
,求实数 的取值范围;
的取值范围; ,顶点A
,顶点A ,
,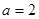 ,求△ABC的面积。
,求△ABC的面积。 中,角
中,角 所对的边分别为a,b, c.
所对的边分别为a,b, c. 且
且 .
. 时,求
时,求 的值;
的值; 为锐角,求p的取值范围
为锐角,求p的取值范围  .
. ,求a,b;
,求a,b;