题目内容
(文)数列{an}的通项公式为an=
|
| lim |
| n→∞ |
分析:由数列的性质可知Sn=1+2+(
)3+ (
)4 +…+(
)n=3+
=
-(
)n-2,由此可以求出
Sn的值.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
1-
|
| 13 |
| 4 |
| 1 |
| 2 |
| lim |
| n→∞ |
解答:解:∵an=
,
∴Sn=1+2+(
)3+ (
)4 +…+(
)n
=3+
=
-(
)n-2
∴
Sn=
[
-(
)n-2]=
.
答案:
.
|
∴Sn=1+2+(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=3+
| ||||
1-
|
=
| 13 |
| 4 |
| 1 |
| 2 |
∴
| lim |
| n→∞ |
| lim |
| n→∞ |
| 13 |
| 4 |
| 1 |
| 2 |
| 13 |
| 4 |
答案:
| 13 |
| 4 |
点评:本题考查数列的性质和数列的极限,解题时要注意数列前n项和的具体求法.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
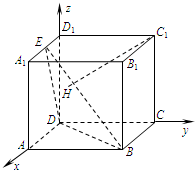 [理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点,
[理]如图,在正方体ABCD-A1B1C1D1中,E是棱A1D1的中点,H为平面EDB内一点, 且{Cn}的前n项和为Tn,求T2n(n∈N*)。
且{Cn}的前n项和为Tn,求T2n(n∈N*)。