题目内容
把一段长为1的篱笆分成两端,分别作为钝角三角形ABC的两边AB和BC,且∠ABC=120°,则三角形面积的最大值为 .
【答案】分析:由正弦定理的面积公式,得三角形的面积S= acsinB=
acsinB=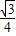 ac,再由a+c=1结合基本不等式,算出ac≤
ac,再由a+c=1结合基本不等式,算出ac≤ ,即可得到当且仅当a=c=
,即可得到当且仅当a=c= 时,三角形面积的最大值
时,三角形面积的最大值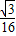 .
.
解答:解:由题意,△ABC中,AB=c,BC=a,满足a+c=1,
可得三角形的面积S= acsinB=
acsinB= ac•
ac•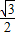 =
=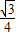 ac
ac
∵a+c≥2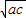 ,可得ac≤
,可得ac≤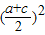 =
=
∴当且仅当a=c= 时,三角形面积的最大值为
时,三角形面积的最大值为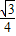 ×
× =
=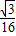
故答案为: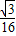
点评:本题给出三角形的两边之和等于1,在夹角为120度的情况下求面积的最大值.着重考查了三角形的面积公式和基本不等式求最值等知识,属于基础题.
 acsinB=
acsinB=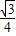 ac,再由a+c=1结合基本不等式,算出ac≤
ac,再由a+c=1结合基本不等式,算出ac≤ ,即可得到当且仅当a=c=
,即可得到当且仅当a=c= 时,三角形面积的最大值
时,三角形面积的最大值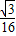 .
.解答:解:由题意,△ABC中,AB=c,BC=a,满足a+c=1,
可得三角形的面积S=
 acsinB=
acsinB= ac•
ac•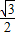 =
=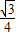 ac
ac∵a+c≥2
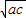 ,可得ac≤
,可得ac≤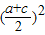 =
=
∴当且仅当a=c=
 时,三角形面积的最大值为
时,三角形面积的最大值为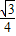 ×
× =
=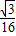
故答案为:
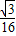
点评:本题给出三角形的两边之和等于1,在夹角为120度的情况下求面积的最大值.着重考查了三角形的面积公式和基本不等式求最值等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目