题目内容
5.求函数$f(x)={x^3}-\frac{3}{2}{x^2}+5$在区间[-2,2]上的最大值与最小值.分析 求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的最值即可.
解答 解:f′(x)=3x2-3x=3x(x-1),
令f′(x)>0,解得:x>1或x<0,
令f′(x)<0,解得:0<x<1,
故f(x)在[-2,0)递增,在(0,1)递减,在(1,2]递增,
而f(-2)=-9,f(0)=5,f(1)=$\frac{9}{2}$,f(2)=7,
故函数f(x)max=7,f(x)min=f(-2)=-9.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.以下四个命题中是假命题的是( )
| A. | “昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿”此推理属于演绎推理. | |
| B. | “在平面中,对于三条不同的直线a,b,c,若a∥b,b∥c则a∥c,将此结论放到空间中也成立”此推理属于合情推理. | |
| C. | “a≤0”是“函数f(x)=ax+lnx存在极值”的必要不充分条件. | |
| D. | 若$x∈(0\;,\;\;\frac{π}{2}]$,则$sinx+\frac{2}{sinx}$的最小值为$2\sqrt{2}$. |
15.已知双曲线${x^2}-\frac{y^2}{b^2}=1({b>0})$,以原点O为圆心,双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A,B,C,D四点,这四点围成的四边形面积为b,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3 | D. | $2\sqrt{2}$ |
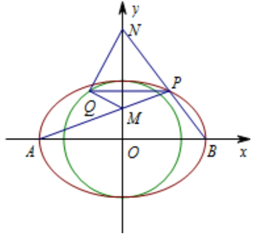 已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.
已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.