题目内容
已知函数
（a＞0，且a≠1）的值域为R，则实数a的取值范围是（ ）A．（0，1）∪（1，2]
B．（2，+∞）
C．（4，+∞）
D．（0，1）∪（1，4]
【答案】分析：利用对数的性质和二次函数的性质等价转化即可求出．
解答：解：函数
（a＞0，且a≠1）的值域为R?y=
（a＞0，且a≠1）的值域为（0，+∞）?y=x2-4x+a（a＞0，且a≠1）的值域为（0，+∞）
?△=（-4）2-4a≥0，a＞0且a≠1．解得0＜a≤4且a≠1．
故选D．
点评：熟练使用对数函数和二次函数的性质进行等价转化是解题的关键．
解答：解：函数
（a＞0，且a≠1）的值域为R?y=（a＞0，且a≠1）的值域为（0，+∞）?y=x2-4x+a（a＞0，且a≠1）的值域为（0，+∞）?△=（-4）2-4a≥0，a＞0且a≠1．解得0＜a≤4且a≠1．
故选D．
点评：熟练使用对数函数和二次函数的性质进行等价转化是解题的关键．
练习册系列答案
相关题目
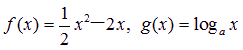（a＞0，且a≠1），其中为常数．如果
是增函数，且
存在零点（
的导函数）．
（
为
的导函数），证明：
．
（a>0，且
，
的定义域； （２）讨论函数
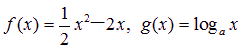（a＞0，且a≠1），其中为常数．如果
是增函数，且
存在零点（
的导函数）．
（
为
的导函数），证明：
．
（a＞0，且a≠1）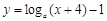
（a > 0，且
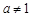）的图象恒过定点A，若点A在直线
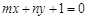上，其中
，
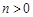，则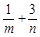
的最小值为__________.