题目内容
4.集合A={x||x-1|<1},B={x|$\frac{2}{x-1}$≥1},C={x|2x2+mx-1<0},若“x∈A∩B”是“x∈C”的充分不必要条件,求m的取值范围.分析 根据不等式的性质求出集合A,B,利用充分条件和必要条件的定义和关系转化为函数关系进行求解即可.
解答 解:A={x||x-1|<1}={x|0<x<2},
B={x|$\frac{2}{x-1}$≥1}={x|$\frac{2}{x-1}$-1=$\frac{3-x}{x-1}$≥0}={x|1<x≤3},
∴A∩B={x|1<x<2}
∵“x∈A∩B”是“x∈C”的充分不必要条件
∴A∩B?C,
设f(x)=2x2+mx-1,
则$\left\{\begin{array}{l}{f(1)≤0}\\{f(2)≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{1+m≤0}\\{8+2m-1=2m-7≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m≤-1}\\{m≤-\frac{7}{2}}\end{array}\right.$,
即m≤-$\frac{7}{2}$,
点评 本题主要考查充分条件和必要条件的应用,利用不等式的解法求出集合的等价条件,将不等式关系转化为集合关系是解决本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
14.在△ABC中,b=3,c=4,B=30°,则此三角形解的情况是( )
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |
12.AB是圆O的直径,点C,D在圆上,且AB=4,∠AOC=∠A0D=120°,点E,F分别在线段上,且$\overrightarrow{OE}$=λ$\overrightarrow{OC}$,$\overrightarrow{OF}$=2λ$\overrightarrow{OD}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的最大值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{15}{4}$ | D. | $\frac{15}{4}$ |
13.点P(x,y)满足平面区域:$\left\{\begin{array}{l}{cosθ≤x≤3cosθ}\\{sinθ≤y≤3sinθ}\end{array}\right.$(θ∈R),点M(x,y)满足:(x+5)2+(y+5)2=1,则|$\overrightarrow{PM}$|的最小值是( )
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{2}$-1 | C. | 6$\sqrt{2}$-1 | D. | $\sqrt{61}$-1 |
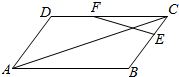 如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$,$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$.
如图,在?ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,$\overrightarrow{CE}$=$\frac{1}{3}$$\overrightarrow{CB}$,$\overrightarrow{CF}$=$\frac{2}{3}$$\overrightarrow{CD}$.