题目内容
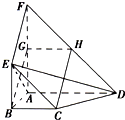
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,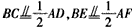 。
。
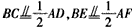 。
。
(1)证明:C,D,F,E四点共面;
(2)设AB=BC=BE,求二面角A-ED-B的大小。
(2)设AB=BC=BE,求二面角A-ED-B的大小。
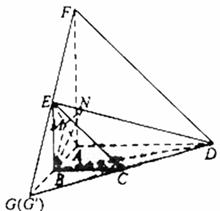
| 解:(1)如图,延长DC交AB的延长线于点G, 由  得 得  延长FE交AB的延长线于G',同理可得  故  即G与G'重合 因此直线CD、EF相交于点G,即C,D,F,E四点共面。 (2)证明:设AB=1,则BC=BE=1,AD=2 如图,取AE中点M,连接BM,则BM⊥AE 又由已知得AD⊥平面ABEF 故AD⊥BM,即BM与平面ADE内两相交直线AD、AE都垂直, 所以BM⊥平面ADE,作MN⊥DE,垂足为N,连接BN 由三垂线定理知BN⊥ED,则∠BNM为二面角A-ED-B的平面角 又  故  所以二面角A-ED-B的大小为  。 。 |
 |

练习册系列答案
相关题目
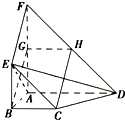 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC 如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC