题目内容
已知:0<α<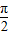 <β<π,cos(β-
<β<π,cos(β-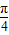 )=
)= ,sin(α+β)=
,sin(α+β)= .
.(1)求sin2β的值;
(2)求cos(α+
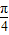 )的值.
)的值.
【答案】分析:(1)法一:直接利用两角差的余弦函数展开,再用方程两边平方,求sin2β的值;
法二:利用sin2β=cos(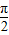 -2β),二倍角公式,直接求出sin2β的值;
-2β),二倍角公式,直接求出sin2β的值;
(2)通过题意求出sin(β-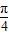 )=
)=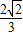 ,cos(α+β)=-
,cos(α+β)=- ,根据cos(α+
,根据cos(α+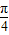 )=cos[(α+β)-(β-
)=cos[(α+β)-(β-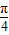 )],展开代入数据,即可求cos(α+
)],展开代入数据,即可求cos(α+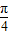 )的值.
)的值.
解答:解:(1)法一:∵cos(β-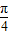 )=cos
)=cos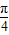 cosβ+sin
cosβ+sin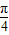 sinβ
sinβ
=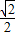 cosβ+
cosβ+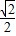 sinβ=
sinβ= .
.
∴cosβ+sinβ=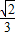 .
.
∴1+sin2β= ,∴sin2β=-
,∴sin2β=- .
.
法二:sin2β=cos(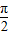 -2β)
-2β)
=2cos2(β-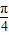 )-1=-
)-1=- .
.
(2)∵0<α<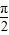 <β<π,∴
<β<π,∴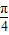 <β-
<β-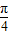 <
<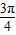 ,
,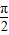 <α+β<
<α+β<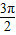 .
.
∴sin(β-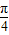 )>0,cos(α+β)<0.
)>0,cos(α+β)<0.
∵cos(β-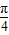 )=
)= ,sin(α+β)=
,sin(α+β)= ,
,
∴sin(β-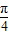 )=
)=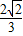 ,cos(α+β)=-
,cos(α+β)=- .
.
∴cos(α+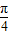 )=cos[(α+β)-(β-
)=cos[(α+β)-(β-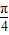 )]
)]
=cos(α+β)cos(β-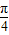 )+sin(α+β)sin(β-
)+sin(α+β)sin(β-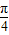 )
)
=- ×
× +
+ ×
×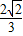 =
=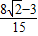 .
.
点评:本题是基础题,考查三角函数的化简与求值,角的变换技巧在三角函数化简求值中应用比较普遍,不仅体现一个人的解题能力,同时体现数学素养的高低,可以说是智慧与能力的展现题目.
法二:利用sin2β=cos(
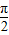 -2β),二倍角公式,直接求出sin2β的值;
-2β),二倍角公式,直接求出sin2β的值;(2)通过题意求出sin(β-
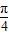 )=
)=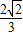 ,cos(α+β)=-
,cos(α+β)=- ,根据cos(α+
,根据cos(α+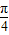 )=cos[(α+β)-(β-
)=cos[(α+β)-(β-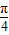 )],展开代入数据,即可求cos(α+
)],展开代入数据,即可求cos(α+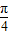 )的值.
)的值.解答:解:(1)法一:∵cos(β-
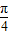 )=cos
)=cos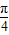 cosβ+sin
cosβ+sin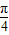 sinβ
sinβ=
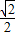 cosβ+
cosβ+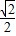 sinβ=
sinβ= .
.∴cosβ+sinβ=
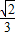 .
.∴1+sin2β=
 ,∴sin2β=-
,∴sin2β=- .
.法二:sin2β=cos(
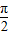 -2β)
-2β)=2cos2(β-
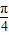 )-1=-
)-1=- .
.(2)∵0<α<
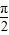 <β<π,∴
<β<π,∴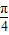 <β-
<β-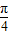 <
<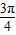 ,
,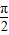 <α+β<
<α+β<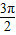 .
.∴sin(β-
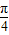 )>0,cos(α+β)<0.
)>0,cos(α+β)<0.∵cos(β-
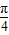 )=
)= ,sin(α+β)=
,sin(α+β)= ,
,∴sin(β-
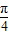 )=
)=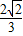 ,cos(α+β)=-
,cos(α+β)=- .
.∴cos(α+
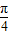 )=cos[(α+β)-(β-
)=cos[(α+β)-(β-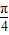 )]
)]=cos(α+β)cos(β-
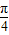 )+sin(α+β)sin(β-
)+sin(α+β)sin(β-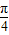 )
)=-
 ×
× +
+ ×
×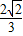 =
=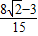 .
.点评:本题是基础题,考查三角函数的化简与求值,角的变换技巧在三角函数化简求值中应用比较普遍,不仅体现一个人的解题能力,同时体现数学素养的高低,可以说是智慧与能力的展现题目.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知α∈(0,π),且sinα+cosα=
,则cosα的值为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|