题目内容
设抛物线y2=8x,O为坐标原点,点A,B是抛物线上的点,
(1)如果OA、OB的斜率分别为![]() ,-2,求直线AB与x轴的交点坐标;
,-2,求直线AB与x轴的交点坐标;
(2)如果OA⊥OB,求证:直线AB必过定点,并求出定点坐标;
解(1)直线OA:![]() 代入
代入![]() 解得
解得![]()
直线OB:![]() 代入
代入![]() 解得
解得![]()
∴AB方程为:![]() 令
令![]() 得
得![]()
∴直-线AB与x轴的交点为![]() -- (3分)
-- (3分)
(2)设AB方程为:![]() ,(
,(![]() 存在)
存在)
由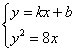 消去
消去![]() 得:
得:
![]() ,-----(4分)
,-----(4分)
(显然![]() )设
)设![]() 则由
则由![]() 得
得
![]() 即
即![]()
得![]()
∴![]() 即
即![]()
∴AB方程为:![]()
∴AB方程恒过定点![]()
当![]() 不存在时容易验证AB方程也过定点
不存在时容易验证AB方程也过定点![]()

练习册系列答案
相关题目
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为-
,那么|PF|=( )
| 3 |
A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |