题目内容
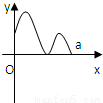
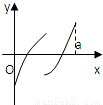
 定义在区间[0,a]上的函数f(x)的图象如右下图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形面积为S(x),则函数S(x)的导函数S'(x)的图象大致是
定义在区间[0,a]上的函数f(x)的图象如右下图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形面积为S(x),则函数S(x)的导函数S'(x)的图象大致是
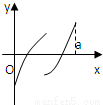
- A.

- B.

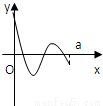
- C.

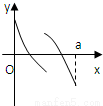
- D.

C
分析:先分析出函数S(x)的表达式为 ,其中AB为定值,h为点C到AB的距离,再利用h在区间[0,a]上的变化情况,得出函数S(x)的增减变化,即可得到其导函数S′(x)的图象.
,其中AB为定值,h为点C到AB的距离,再利用h在区间[0,a]上的变化情况,得出函数S(x)的增减变化,即可得到其导函数S′(x)的图象.
解答: 如图,连接AB,BC,AC
如图,连接AB,BC,AC
设点C到AB的距离为h,则△ABC的面积 ,其中AB为定值
,其中AB为定值
当点C沿着曲线从A运动到B,h是连续变化,这样S(x)也是连续变化,所以面积函数S(x)肯定在[0,a]上可导,且其导数是连续的.从而排除B和D;
当x∈(0,m]时,点C从点A出发,距离h越来越大,故S(x)递增,所以S'(x)>0;
当x∈(m,n]时,距离h越来越小,故S(x)递减,所以S'(x)<0;
当x∈(n,e]时,距离h越来越大,故S(x)递增,所以S'(x)>0;
当x∈(e,a]时,距离h越来越小,故S(x)递减,所以S'(x)<0.
故选C
点评:本题主要考查导函数与原函数单调性之间的关系.
分析:先分析出函数S(x)的表达式为
 ,其中AB为定值,h为点C到AB的距离,再利用h在区间[0,a]上的变化情况,得出函数S(x)的增减变化,即可得到其导函数S′(x)的图象.
,其中AB为定值,h为点C到AB的距离,再利用h在区间[0,a]上的变化情况,得出函数S(x)的增减变化,即可得到其导函数S′(x)的图象.解答:
 如图,连接AB,BC,AC
如图,连接AB,BC,AC设点C到AB的距离为h,则△ABC的面积
 ,其中AB为定值
,其中AB为定值当点C沿着曲线从A运动到B,h是连续变化,这样S(x)也是连续变化,所以面积函数S(x)肯定在[0,a]上可导,且其导数是连续的.从而排除B和D;
当x∈(0,m]时,点C从点A出发,距离h越来越大,故S(x)递增,所以S'(x)>0;
当x∈(m,n]时,距离h越来越小,故S(x)递减,所以S'(x)<0;
当x∈(n,e]时,距离h越来越大,故S(x)递增,所以S'(x)>0;
当x∈(e,a]时,距离h越来越小,故S(x)递减,所以S'(x)<0.
故选C
点评:本题主要考查导函数与原函数单调性之间的关系.

练习册系列答案
相关题目
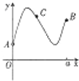
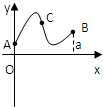 定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )
定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )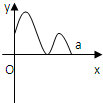
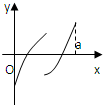
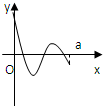
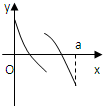
 定义在区间[0,a]上的函数f(x)的图象如右下图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形面积为S(x),则函数S(x)的导函数S'(x)的图象大致是( )
定义在区间[0,a]上的函数f(x)的图象如右下图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形面积为S(x),则函数S(x)的导函数S'(x)的图象大致是( )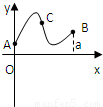 定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )
定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )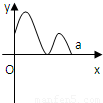


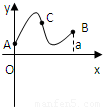 定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )
定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )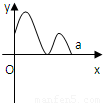
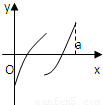
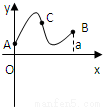 定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )
定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( )