题目内容
已知函数![]() .
.
(Ⅰ)求函数f(x)的最小值;
(Ⅱ)证明:对任意m,n∈(0,+∞),都有f(m)≥g(n)成立.
考点:
导数在最大值、最小值问题中的应用;利用导数求闭区间上函数的最值.
专题:
导数的综合应用.
分析:
(I)利用导数的运算法则可得f′(x)=lnx+1(x>0),进而得到当![]() 时与当
时与当![]() 时,函数f(x)的单调性及极小值,也即最小值.
时,函数f(x)的单调性及极小值,也即最小值.
(II)由(I)可知:![]() .同理利用导数即可得到g(x)的极大值即最大值.只要证明对任意n∈(0,+∞),都有
.同理利用导数即可得到g(x)的极大值即最大值.只要证明对任意n∈(0,+∞),都有![]() 即可.
即可.
解答:
(I)解:∵f(x)=xlnx,∴f′(x)=lnx+1(x>0),
当![]() 时,f′(x)<0,函数f(x)单调递减;
时,f′(x)<0,函数f(x)单调递减;
当![]() 时,f′(x)>0,函数f(x)单调递增.
时,f′(x)>0,函数f(x)单调递增.
因此,当x=![]() 时,函数f(x)取得极小值,也即最小值,
时,函数f(x)取得极小值,也即最小值,![]() =
=![]() =﹣
=﹣![]() .
.
(II)证明:由(I)可知:![]() .
.
由g(x)=![]() ,得
,得![]() .
.
当x∈(0,1)时,g′(x)>0,函数g(x)单调递增;
当x∈(1,+∞)时,g′(x)<0,函数g(x)单调递减.
∴函数g(x)在x=1时取得极大值即最大值,![]() .
.
∴对任意m,n∈(0,+∞),都有f(m)≥g(n)成立.
点评:
熟练掌握利用导数研究函数的单调性、极值与最值等是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.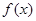 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求