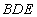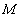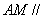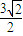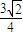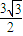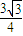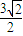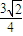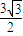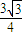题目内容
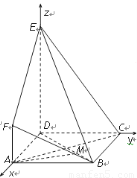
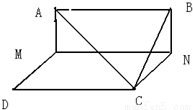
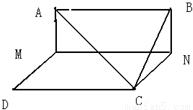
 如图,边长为3正方形ABCD,动点M,N在AD,BC上,且MN∥CD,沿MN将正方形折成直二面角,设AM=x,则点M到平面ABC的距离的最大值为( )
如图,边长为3正方形ABCD,动点M,N在AD,BC上,且MN∥CD,沿MN将正方形折成直二面角,设AM=x,则点M到平面ABC的距离的最大值为( )分析:过M作ME⊥AC,垂足为E,则ME⊥平面ABC,从而点M到平面ABC的距离为ME,在△AMC中,利用基本不等式可求.
解答:解:由题意,过M作ME⊥AC,垂足为E,则ME⊥平面ABC,
在△AMC中,ME=
=
≤
≤
=
当且仅当,x=3-x,即x=
时,ME的最大值为
故选B.
在△AMC中,ME=
| x(3-x) | ||
|
| 1 | ||||||
|
| ||
|
| ||
|
3
| ||
| 4 |
当且仅当,x=3-x,即x=
| 3 |
| 2 |
3
| ||
| 4 |
故选B.
点评:本题以图形的翻折为载体,考查点面距离,关键是搞清图形翻折前后图形的变与不变,同时注意利用基本不等式求最值.

练习册系列答案
相关题目