题目内容
如图(一),在直角梯形ABCD中,AD∥BC,AB⊥AD,AD=2AB=2BC,E为AD中点,沿CE折叠,使面DEC⊥面ABCE,在图(二)中.
(I)证明:AC⊥BD
(Ⅱ)求DE与面ACD所成角的余弦值.
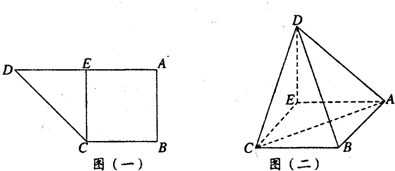
(I)证明:如图所示,以E为坐标原点,建立空间直角坐标系,令AB=a,则E(0,0,0),C(a,0,0),A(0,a,0),D(0,0,a),B(a,a,0),
∴ ,
,
∵

∴ ,
,
∴AC⊥BD
(Ⅱ)设面ACD的法向量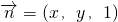
∴ ,∴
,∴ ,∴
,∴
∴cos
∴DE与面ACD所成角的余弦值为
分析:(I)以E为坐标原点,建立空间直角坐标系,令AB=a,用坐标表示点与向量,证明 即可;
即可;
(Ⅱ)求出面ACD的法向量 ,计算cos
,计算cos ,即可得到DE与面ACD所成角的余弦值.
,即可得到DE与面ACD所成角的余弦值.
点评:本题考查平面图形的翻折,考查利用空间向量解决立体几何问题,关键是建系设点.
∴
 ,
,
∵


∴
 ,
,∴AC⊥BD
(Ⅱ)设面ACD的法向量
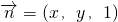
∴
 ,∴
,∴ ,∴
,∴
∴cos

∴DE与面ACD所成角的余弦值为

分析:(I)以E为坐标原点,建立空间直角坐标系,令AB=a,用坐标表示点与向量,证明
 即可;
即可;(Ⅱ)求出面ACD的法向量
 ,计算cos
,计算cos ,即可得到DE与面ACD所成角的余弦值.
,即可得到DE与面ACD所成角的余弦值.点评:本题考查平面图形的翻折,考查利用空间向量解决立体几何问题,关键是建系设点.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AB=3,∠ABC=60°,将此梯形以AD所在直线为轴旋转一周,所得几何体的表面积是( )
如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AB=3,∠ABC=60°,将此梯形以AD所在直线为轴旋转一周,所得几何体的表面积是( )| A、46π | B、23π | C、26π | D、36π |
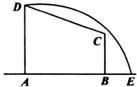 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=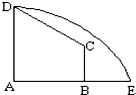 如图在直角梯形ABCD中,AD=3,AB=4,BC=
如图在直角梯形ABCD中,AD=3,AB=4,BC= 如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD⊥AB,BC⊥AB,AD=3,AB=4,BC=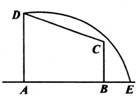 如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=,曲线段DE上任一点到A、B两点的距离之和都相等.
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=,曲线段DE上任一点到A、B两点的距离之和都相等.