题目内容
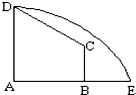 如图在直角梯形ABCD中,AD=3,AB=4,BC=
如图在直角梯形ABCD中,AD=3,AB=4,BC=| 3 |
(1)建立适当的坐标系,求曲线DE的方程;
(2)过C点作一条与曲线DE相交且以C为中点的弦,求出弦所在直线的方程.
分析:(1)由题意,先建立平面直角坐标系,利用曲线的方程这一概念求其动点的轨迹方程,要注意求解方程之后要有题意去掉不符合题意的点;
(2)设出直线方程,联立椭圆方程,结合方程的根与系数关系及中点坐标公式可求斜率k,进而可求直线方程
(2)设出直线方程,联立椭圆方程,结合方程的根与系数关系及中点坐标公式可求斜率k,进而可求直线方程
解答:解:(1)以直线AB为x轴,线段AB的中点为原点建立直角坐标系,
则A(-2,0),B(2,0),C(2,
),D(-2,3).
依题意,曲线段DE是以A、B为焦点的椭圆的一部分.
∵a=
(|AD|+|BD|)=4,c=2,b2=12,
∴所求方程为
+
=1(-2≤x≤4,0≤y≤2
).
(2)设直线方程y-
=k(x-2),即y=k(x-2)+
,将其代入
+
=1
得(3+4k2)x2+(8
k-16k2)x+16k2-16
k-36=0
设弦的端点为M(x1,y1),N(x2,y2),则由
=2,知x1+x2=4,
∴-
=4,解得k=-
.
∴弦MN所在直线方程为y=-
x+2
,验证得知,这时M(0,2
),N(4,0)适合条件.
故这样的直线存在,其方程为y=-
x+2
.
则A(-2,0),B(2,0),C(2,
| 3 |
依题意,曲线段DE是以A、B为焦点的椭圆的一部分.
∵a=
| 1 |
| 2 |
∴所求方程为
| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
(2)设直线方程y-
| 3 |
| 3 |
| x2 |
| 16 |
| y2 |
| 12 |
得(3+4k2)x2+(8
| 3 |
| 3 |
设弦的端点为M(x1,y1),N(x2,y2),则由
| x1+x2 |
| 2 |
∴-
8
| ||
| 3+4k2 |
| ||
| 2 |
∴弦MN所在直线方程为y=-
| ||
| 2 |
| 3 |
| 3 |
故这样的直线存在,其方程为y=-
| ||
| 2 |
| 3 |
点评:(1)考查了利用曲线的方程这一概念,先建立平面直角坐标系,然后利用定义法求其动点的轨迹方程,但要注意去掉不符合条件的点
(2)本题主要考查了直线与椭圆相交关系的应用,方程的根与系数关系及中点坐标公式的应用,要注意”设而不求“方法的应用.
(2)本题主要考查了直线与椭圆相交关系的应用,方程的根与系数关系及中点坐标公式的应用,要注意”设而不求“方法的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
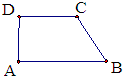 如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AB=3,∠ABC=60°,将此梯形以AD所在直线为轴旋转一周,所得几何体的表面积是
如图,在直角梯形ABCD中,AB∥CD,AB⊥AD,CD=2,AB=3,∠ABC=60°,将此梯形以AD所在直线为轴旋转一周,所得几何体的表面积是 (2012•福建模拟)在直角梯形ABCD中,AD∥BC,BC=2AD=2AB=2
(2012•福建模拟)在直角梯形ABCD中,AD∥BC,BC=2AD=2AB=2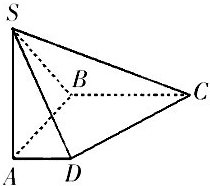 如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,
如图在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,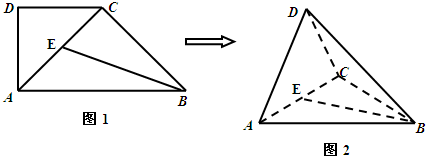 (1)求证:DA⊥BC;
(1)求证:DA⊥BC; (2011•合肥三模)如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上点,且AM=BN,将三角形ADE沿AE折起.下列说法正确的是
(2011•合肥三模)如图,在直角梯形ABCD中,AB∥DC,AE⊥DC,BE∥AD.M、N分别是AD、BE上点,且AM=BN,将三角形ADE沿AE折起.下列说法正确的是