题目内容

若|
AB
|=8，|
AC
|=5，则|
BC
|的取值范围是（　　）
分析：根据平面向量减法法则，得
BC
=
AC
-
AB
，从而将
BC
2化简整理得
BC
2=89-2
AC
•
AB
．讨论
AC
、
AB
夹角可得-40≤
AC
•
AB
≤40，由此代入前面的式子即可得到
BC
2的取值范围，进而得到|
BC
|的取值范围．
解答：解：∵
BC
=
AC
-
AB

∴
BC
2=（
AC
-
AB
）2=
AC
2-2
AC
•
AB
+
AB
2
∵|
AB
|=8且|
AC
|=5
∴
BC
2=（
AC
-
AB
）2=64-2
AC
•
AB
+25=89-2
AC
•
AB

∵-40≤
AC
•
AB
≤40，
当
AC
、
AB
夹角为180°时，左边取等号；当
AC
、
AB
夹角为0°时，右边取等号
可得-80≤-2
AC
•
AB
≤80
∴
BC
2=89-2
AC
•
AB
∈[9，169]
由此可得|
BC
|的取值范围是[3，13]
故选：A
点评：本题给出向量
AC
、
AB
的模，求向量
BC
模的取值范围，着重考查了平面向量减法法则和平面向量数量积的运算性质等知识，属于基础题．
练习册系列答案
相关题目
已知抛物线y2=ax的焦点为F（1，0），过焦点F的直线l交抛物线于A、B两点，若AB=8，则直线l的方程是
 
．
已知抛物线y2=2px（p＞0）上有一点Q（4，m）到焦点F的距离为5，
（1）求p及m的值．
（2）过焦点F的直线L交抛物线于A，B两点，若|AB|=8，求直线L的方程．
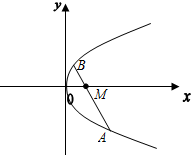如图，M（a，0）（a＞0）是抛物线y2=4x对称轴上一点，过M作抛物线的弦AMB，交抛物线与A，B．
（1）若a=2，求弦AB中点的轨迹方程；
（2）若AB=8，求a的取值范围．
在平面直角坐标系xOy中，直线l过抛物线y2=4x的焦点F交抛物线于A、B两点．
（1）若|AB|=8，求直线l的斜率
（2）若|AF|=m，|BF|=n．求证
1
m
+
1
n
为定值．
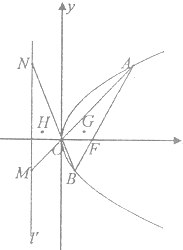过点F（1，0）的直线l交抛物线C：y2=4x于A，B两点．
（1）若|AB|=8，求直线l的方程；
（2）记抛物线C的准线为l，设OA，OB分别交l于M，N两点，△AOB与△MON的重心分别为G，H，求|GH|的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网