题目内容
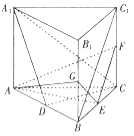
【题目】如图，直三棱柱
的底面为正三角形，
、
、
分别是
、
、
的中点．
⑴若
，求证：
平面
；
⑵若
为
中点，
，四棱锥
的体积为
，求三棱锥
的表面积．
【答案】⑴证明见解析；⑵
．
【解析】
试题分析：⑴由三棱柱
是直三棱柱
，又
， 
平面
，又四边形
为正方形
，又
以
平面
；⑵由
是正三角形
，又
平面
．设
，由
．又
．
试题解析： ⑴证明：如图，因为三棱柱是直三棱柱，所以，
又
是正三角形
的边
的中点，所以，又，
所以平面，则，……………………3分
连接
，易知四边形为正方形，则
，
又，则，因为
，所以平面．……6分
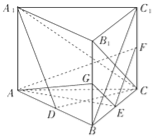
⑵解：因为是正三角形，所以，
又三棱柱
是直三棱柱，所以，
所以平面，所以．………………………………7分
设，由题可知，，所以．………………8分
在
中，，
所以
，∴．……10分
故三棱锥
的表面积
．……12分
练习册系列答案
相关题目
