题目内容
(下列两题中任选一题,都做的以第一小题为准)
(1)用黄金分别割法选取试点的过程中,若试验区间为[3,5],则第二试点应选取的值为________.
(2)设点A,B分别在曲线 (θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
解:(1)由已知试验范围为[3,5],可得区间长度为2,
利用0.618法选取试点:x1=3+0.618×(5-3)=4.236,x2=3+5-4.236=3.764,
(2) (θ为参数) 消去参数θ得,(x-3)2+y2=1
(θ为参数) 消去参数θ得,(x-3)2+y2=1
而ρ=1,而ρ2=x2+y2,
则直角坐标方程为x2+y2=1,
点A在圆(x-3)2+y2=1上,点B在圆x2+y2=1上
则|AB|的最小值为3-1-1=1
故答案为:3.764;1.
分析:(1)先由已知试验范围为[3,5],可得区间长度为2,再利用0.618法选取试点,从而得出x2即可.
(2)先根据ρ2=x2+y2,sin2+cos2θ=1将极坐标方程和参数方程化成直角坐标方程,根据当两点连线经过两圆心时|AB|的最小,从而最小值为两圆心距离减去两半径.
点评:(1)本小题考查的是黄金分割法-0.618法的简单应用.解答的关键是要了解黄金分割法0.618法.
(2)本题主要考查了参数方程化成普通方程,以及简单曲线的极坐标方程等有关知识,同时考查了转化与划归的思想,属于基础题.
利用0.618法选取试点:x1=3+0.618×(5-3)=4.236,x2=3+5-4.236=3.764,
(2)
 (θ为参数) 消去参数θ得,(x-3)2+y2=1
(θ为参数) 消去参数θ得,(x-3)2+y2=1而ρ=1,而ρ2=x2+y2,
则直角坐标方程为x2+y2=1,
点A在圆(x-3)2+y2=1上,点B在圆x2+y2=1上
则|AB|的最小值为3-1-1=1
故答案为:3.764;1.
分析:(1)先由已知试验范围为[3,5],可得区间长度为2,再利用0.618法选取试点,从而得出x2即可.
(2)先根据ρ2=x2+y2,sin2+cos2θ=1将极坐标方程和参数方程化成直角坐标方程,根据当两点连线经过两圆心时|AB|的最小,从而最小值为两圆心距离减去两半径.
点评:(1)本小题考查的是黄金分割法-0.618法的简单应用.解答的关键是要了解黄金分割法0.618法.
(2)本题主要考查了参数方程化成普通方程,以及简单曲线的极坐标方程等有关知识,同时考查了转化与划归的思想,属于基础题.

练习册系列答案
相关题目
 请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
请考生在下列两题中任选一题作答,若两题都做,则按所做的第一题评阅计分.
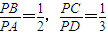 ,则
,则 的值为 .
的值为 .
 (t为参数)距离的最大值为 .
(t为参数)距离的最大值为 .