题目内容
在直角坐标系中,有四点A(-1,2),B (0,1),C (1,2),D (x,y)同时位于一条拋物线上,则x与y满足的关系式是________.
y=x2+1
分析:由于A(-1,2),C (1,2),两点关于y轴对称,结合抛物线的对称性可知:此抛物线的对称轴是y轴,故设抛物线的方程为y=ax2+c,将A,B 两点的坐标代入即可求得x与y满足的关系式.
解答:由于A(-1,2),C (1,2),两点关于直线x=0对称,
根据抛物线的对称性可知:
此抛物线的对称轴是y轴,故设抛物线的方程为
y=ax2+c,
将A(-1,2),B (0,1),两点的坐标代入得:

∴
则x与y满足的关系式是y=x2+1.
故答案为:y=x2+1.
点评:本题主要考查了抛物线的方程的求法,以及抛物线的对称性,解答的关键是发现题中给出的三点中有两点关于y轴对称,从而设出方程.
分析:由于A(-1,2),C (1,2),两点关于y轴对称,结合抛物线的对称性可知:此抛物线的对称轴是y轴,故设抛物线的方程为y=ax2+c,将A,B 两点的坐标代入即可求得x与y满足的关系式.
解答:由于A(-1,2),C (1,2),两点关于直线x=0对称,
根据抛物线的对称性可知:
此抛物线的对称轴是y轴,故设抛物线的方程为
y=ax2+c,
将A(-1,2),B (0,1),两点的坐标代入得:

∴

则x与y满足的关系式是y=x2+1.
故答案为:y=x2+1.
点评:本题主要考查了抛物线的方程的求法,以及抛物线的对称性,解答的关键是发现题中给出的三点中有两点关于y轴对称,从而设出方程.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)
附加题:(选做题:在下面A、B、C、D四个小题中只能选做两题)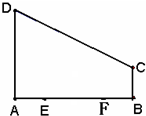 如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ.
如图直角梯形ABCD中,∠DAB=90°,AD∥BC,E,F是AB边的四等分点,AB=4,BC=BF=AE=1,AD=3,P为在梯形区域内一动点,满足PE+PF=AB,记动点P的轨迹为Γ. 之间的“直角距离”为
之间的“直角距离”为 ,
, ,则
,则 为定值;
为定值; 表示
表示 两点间的“直线距离”,那么
两点间的“直线距离”,那么 ;
; 为直线
为直线 上任一点,
上任一点, 为坐标原点,则
为坐标原点,则 ;
; 三点不共线,则必有
三点不共线,则必有 .
.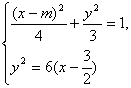 (其中θ为参数)和抛物线
(其中θ为参数)和抛物线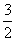 (其中t为参数).
(其中t为参数).