题目内容
(14分)设函数![]()
(Ⅰ)若![]() 互不相等,且
互不相等,且![]() ,求证
,求证![]() 成等差数列;
成等差数列;
(Ⅱ)若![]() ,过两点
,过两点![]() 的中点作与x轴垂直的直线,此直线与
的中点作与x轴垂直的直线,此直线与![]() 的图象交于点P,
的图象交于点P,
求证:函数![]() 在点P处的切线过点(c,0);
在点P处的切线过点(c,0);
(Ⅲ)若c=0, ![]() ,
,![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解析:(Ⅰ)![]()
若![]() ,则
,则![]()
![]()
![]() 即
即![]() ∴
∴![]() 成等差数列……………3分
成等差数列……………3分
(Ⅱ)依题意![]()

∴切线![]()
令![]() 得
得![]() ,即
,即![]()
∴切线过点![]() .………………………………………………………8分
.………………………………………………………8分
(Ⅲ)![]() ,则
,则![]()
∴![]()
①![]() 时:
时:
![]() 时,
时,![]() ,此时
,此时![]() 为增函数;
为增函数;
![]() 时,
时,![]() ,此时
,此时![]() 为减函数;
为减函数;
![]() 时,
时,![]() ,此时
,此时![]() 为增函数.
为增函数.
而![]() ,依题意有
,依题意有
![]() ………………10分
………………10分
②![]() 时:
时:![]() 在
在![]() 时,
时,![]()
∴![]() 即
即![]() ……(☆)
……(☆)
记![]() ,则
,则![]()
∴![]() 为R上的增函数,而
为R上的增函数,而![]() ,∴
,∴![]() 时,
时,
![]() 恒成立,(☆)无解.
恒成立,(☆)无解.

练习册系列答案
相关题目
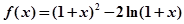 .
.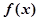 的单调区间;
的单调区间;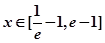 时,(其中
时,(其中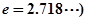 不等式
不等式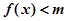 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;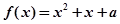 在区间[0,2]上的根的个数.
在区间[0,2]上的根的个数. =
= ,
,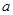 ∈R
∈R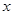 =
=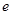 为
为 的极值点,求实数
的极值点,求实数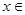 (0,3
(0,3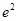 成立.
成立.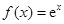 (
(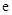 为自然对数的底数),
为自然对数的底数),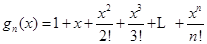 (
(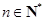 ).
).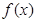
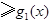 ;
;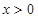 时,比较
时,比较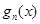 的大小,并说明理由;
的大小,并说明理由; (
( ).
). ,
, ,当
,当 时,
时,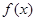 取得极值。
取得极值。 的值;
的值; 时,函数
时,函数 的图象有三个公共点,求
的图象有三个公共点,求 的取值范围。
的取值范围。