题目内容
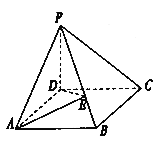
【题目】如图在棱锥
中， 
为矩形， 
面
， 
， 
与面
成
角， 
与面
成
角.
（1）在
上是否存在一点
，使
面
，若存在确定
点位置，若不存在，请说明理由；
（2）当
为
中点时，求二面角
的余弦值.
【答案】（1）见解析（2）
【解析】试题分析：（1）法一：要证明PC⊥面ADE，只需证明AD⊥PC，通过证明
即可，然后推出存在点E为PC中点．
法二：建立如图所示的空间直角坐标系D﹣XYZ，设
，通过
得到
，即存在点E为PC中点．
（2）由（1）知求出面ADE的法向量，面PAE的法向量，利用空间向量的数量积．求解二面角P﹣AE﹣D的余弦值．
试题解析：
（Ⅰ）法一：要证明PC⊥面ADE，易知AD⊥面PDC，即得AD⊥PC，故只需
即可，所以由
,即存在点E为PC中点
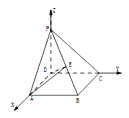
法二：建立如图所示的空间直角坐标系D－XYZ，
由题意知PD＝CD＝1，
，设
， 
，
,
由
，得
，
即存在点E为PC中点。
（Ⅱ）由（Ⅰ）知
， 
， 
， 
， 
， 
， 
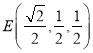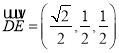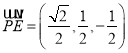
设面ADE的法向量为
，面PAE的法向量为
由的法向量为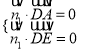
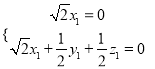得， 
得
同理求得
所以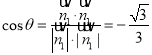
故所求二面角P－AE－D的余弦值为
.
练习册系列答案
名校课堂系列答案
相关题目
