题目内容
在△ABC中,已知A=30°,a=8,b= ,则△ABC的面积为
,则△ABC的面积为
- A.

- B.16
- C.
 或16
或16 - D.
 或
或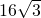
D
分析:由已知中,在△ABC中,已知A=30°,a=8,b= ,由余弦定理,我们可以求出c的值,代入S△ABC=
,由余弦定理,我们可以求出c的值,代入S△ABC= •bc•sinA,即可求出△ABC的面积.
•bc•sinA,即可求出△ABC的面积.
解答:∵在△ABC中,已知A=30°,a=8,b= ,
,
由余弦定理cosA= 得:
得:
cos30°= =
=
解得:c=16或c=8
又∵S△ABC= •bc•sinA
•bc•sinA
∴S△ABC=32 ,或S△ABC=16
,或S△ABC=16
故选D.
点评:本题考查的知识点是三角形中的几何计算,余弦定理,三角形面积公式,其中根据已知利用余弦定理求出c的值,是解答本题的关键.
分析:由已知中,在△ABC中,已知A=30°,a=8,b=
 ,由余弦定理,我们可以求出c的值,代入S△ABC=
,由余弦定理,我们可以求出c的值,代入S△ABC= •bc•sinA,即可求出△ABC的面积.
•bc•sinA,即可求出△ABC的面积.解答:∵在△ABC中,已知A=30°,a=8,b=
 ,
,由余弦定理cosA=
 得:
得:cos30°=
 =
=
解得:c=16或c=8
又∵S△ABC=
 •bc•sinA
•bc•sinA∴S△ABC=32
 ,或S△ABC=16
,或S△ABC=16
故选D.
点评:本题考查的知识点是三角形中的几何计算,余弦定理,三角形面积公式,其中根据已知利用余弦定理求出c的值,是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目