题目内容
已知函数
(Ⅰ)求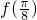 的值;
的值;
(Ⅱ)求函数f(x)的最小正周期及单调递减区间.
(本小题满分13分)
解:(Ⅰ)因为 =2cos2x+sin2x…(2分)
=2cos2x+sin2x…(2分)
=1+cos2x+sin2x…(4分)
= …(6分)
…(6分)
所以 …(7分)
…(7分)
(Ⅱ)因为
所以 …(9分)
…(9分)
又y=sinx的单调递减区间为 ,(k∈Z)…(10分)
,(k∈Z)…(10分)
所以令 …(11分)
…(11分)
解得 …(12分)
…(12分)
所以函数f(x)的单调减区间为 ,(k∈Z)…(13分)
,(k∈Z)…(13分)
分析:(Ⅰ)通过二倍角公式以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求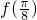 的值;
的值;
(Ⅱ)直接利用正弦函数的周期的求法,以及三角函数的单调性直接求函数f(x)的单调递减区间.
点评:本题考查两角和的正弦函数与二倍角公式的应用,三角函数的周期的求法,单调区间的求法,考查计算能力.
解:(Ⅰ)因为
 =2cos2x+sin2x…(2分)
=2cos2x+sin2x…(2分)=1+cos2x+sin2x…(4分)
=
 …(6分)
…(6分)所以
 …(7分)
…(7分)(Ⅱ)因为

所以
 …(9分)
…(9分)又y=sinx的单调递减区间为
 ,(k∈Z)…(10分)
,(k∈Z)…(10分)所以令
 …(11分)
…(11分)解得
 …(12分)
…(12分)所以函数f(x)的单调减区间为
 ,(k∈Z)…(13分)
,(k∈Z)…(13分)分析:(Ⅰ)通过二倍角公式以及两角和的正弦函数化简函数为一个角的一个三角函数的形式,然后求
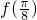 的值;
的值;(Ⅱ)直接利用正弦函数的周期的求法,以及三角函数的单调性直接求函数f(x)的单调递减区间.
点评:本题考查两角和的正弦函数与二倍角公式的应用,三角函数的周期的求法,单调区间的求法,考查计算能力.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
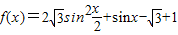 .
.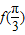 的值;
的值;
 .
. 的值;
的值; ,都有f(x)≤c,求实数c的取值范围.
,都有f(x)≤c,求实数c的取值范围.
 的值;
的值; 的最大值和最小值。
的最大值和最小值。