题目内容
已知函数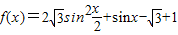 .
.(Ⅰ)求
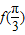 的值;
的值;(Ⅱ)求f(x)的单调递增区间;
(Ⅲ)作出f(x)在一个周期内的图象.

【答案】分析:(Ⅰ)把x= 直接代入函数的解析式,求得函数的值.
直接代入函数的解析式,求得函数的值.
(Ⅱ)利用两角和差的正弦公式化简函数的解析式,再利用正弦函数的单调性求出它的增区间.
(Ⅲ)用五点法作函数y=Asin(ωx+∅)在一个周期上的简图.
解答:解:(Ⅰ)由已知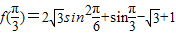 …(2分)
…(2分)
=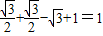 .…(4分)
.…(4分)
(Ⅱ)∵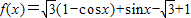 …(6分)
…(6分)
=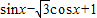 =
=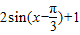 .…(7分)
.…(7分)
∵函数y=sinx的单调递增区间为 ,…(8分)
,…(8分)
由 ,得
,得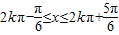 .
.
所以f(x)的单调递增区间为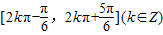 .…(9分)
.…(9分)
(Ⅲ)列表:
作出f(x)在一个周期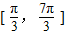 上的图象如图所示.…(12分)
上的图象如图所示.…(12分)
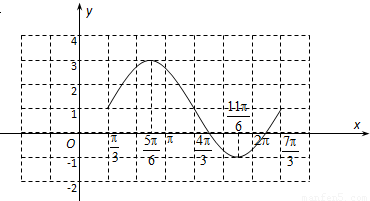
点评:本题主要考查用五点法作函数y=Asin(ωx+∅)在一个周期上的简图,两角和差的正弦公式,正弦函数的单调性,属于中档题.
 直接代入函数的解析式,求得函数的值.
直接代入函数的解析式,求得函数的值.(Ⅱ)利用两角和差的正弦公式化简函数的解析式,再利用正弦函数的单调性求出它的增区间.
(Ⅲ)用五点法作函数y=Asin(ωx+∅)在一个周期上的简图.
解答:解:(Ⅰ)由已知
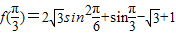 …(2分)
…(2分)=
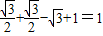 .…(4分)
.…(4分)(Ⅱ)∵
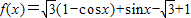 …(6分)
…(6分)=
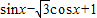 =
=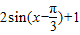 .…(7分)
.…(7分)∵函数y=sinx的单调递增区间为
 ,…(8分)
,…(8分)由
 ,得
,得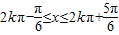 .
.所以f(x)的单调递增区间为
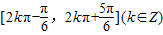 .…(9分)
.…(9分)(Ⅲ)列表:
| x | 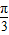 | 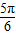 | 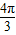 |  | 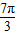 |
x-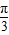 | 0 | 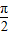 | π | 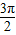 | 2π |
2sin(x-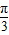 ) ) | 0 | 2 | 0 | -2 | 0 |
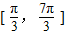 上的图象如图所示.…(12分)
上的图象如图所示.…(12分)
点评:本题主要考查用五点法作函数y=Asin(ωx+∅)在一个周期上的简图,两角和差的正弦公式,正弦函数的单调性,属于中档题.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
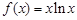 .
.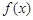 的最小值;
的最小值;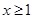 都有
都有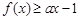 ,求实数
,求实数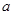 的取值范围.
的取值范围.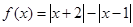
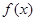 的值域;
的值域;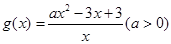 ,若对
,若对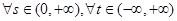 恒有
恒有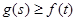 成立,试求实数
成立,试求实数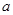 的取值氛围。
的取值氛围。 ,(1)求
,(1)求 的定义域;
的定义域; 是第四象限的角,且
是第四象限的角,且 ,求
,求 的值。
的值。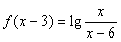 ,
,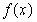 的解析式;
的解析式; .
.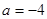 时,求
时,求 的最小值;
的最小值;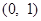 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;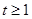 时,不等式
时,不等式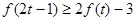 恒成立,求实数
恒成立,求实数