题目内容
(2009•台州一模)在△ABC中,a,b,c是角A,B,C所对的边,已知4cosBsin2
+cos2B=0.
(Ⅰ)求角B的大小;
(Ⅱ)若a=4,△ABC的面积为5
,求b的值.
| B |
| 2 |
(Ⅰ)求角B的大小;
(Ⅱ)若a=4,△ABC的面积为5
| 3 |
分析:(1)△ABC中,由已知条件可得 2cosB(1-cosB)+2cos2B-1=0,解得cosB 的值,即可得到 B 的值.
(2)由
ac•sinB=5
,求得 c=5,再由余弦定理求得 b的值.
(2)由
| 1 |
| 2 |
| 3 |
解答:解:(1)△ABC中,由已知条件可得 2cosB(1-cosB)+2cos2B-1=0,解得cosB=
,故 B=
.(7分)
(2)由
ac•sinB=5
,求得 c=5,(10分)
再由余弦定理得 b2=16+25-2×4×5×
=21,解得 b=
.(14分)
| 1 |
| 2 |
| π |
| 3 |
(2)由
| 1 |
| 2 |
| 3 |
再由余弦定理得 b2=16+25-2×4×5×
| 1 |
| 2 |
| 21 |
点评:本题主要考查二倍角公式、余弦定理的应用,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
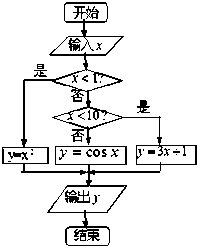 (2009•台州一模)根据右边程序框图,若输出y的值是4,则输入的实数x=
(2009•台州一模)根据右边程序框图,若输出y的值是4,则输入的实数x=