题目内容
(理科)若数列 的前n项和
的前n项和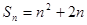 ,若
,若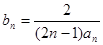 ,记数列
,记数列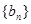 的前n项和为
的前n项和为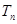 ,则使
,则使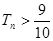 成立的最小正整数n的值为
成立的最小正整数n的值为
5
解析试题分析: .所以
.所以 ,所以
,所以 ,所以
,所以 ,
,
所以使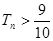 成立的最小正整数n的值为5.
成立的最小正整数n的值为5.
考点:求数列的通项,裂项求和,分式不等式的解法。
点评:.先由Sn求出an是解决本小题的突破口,然后根据 确定应采用裂项求和的方法求出Tn,再解关于n的不等式即可求出n的最小值。
确定应采用裂项求和的方法求出Tn,再解关于n的不等式即可求出n的最小值。

练习册系列答案
相关题目
题目内容
(理科)若数列 的前n项和
的前n项和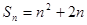 ,若
,若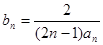 ,记数列
,记数列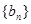 的前n项和为
的前n项和为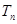 ,则使
,则使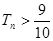 成立的最小正整数n的值为
成立的最小正整数n的值为
5
解析试题分析: .所以
.所以 ,所以
,所以 ,所以
,所以 ,
,
所以使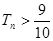 成立的最小正整数n的值为5.
成立的最小正整数n的值为5.
考点:求数列的通项,裂项求和,分式不等式的解法。
点评:.先由Sn求出an是解决本小题的突破口,然后根据 确定应采用裂项求和的方法求出Tn,再解关于n的不等式即可求出n的最小值。
确定应采用裂项求和的方法求出Tn,再解关于n的不等式即可求出n的最小值。
